Question

A tree stands vertical, on the hill side, which makes an angle of \[{22^0}\]with the horizontal. From the point 35 meters directly down the hill from the base of the tree, the angle of elevation of the top of the tree is \[{45^0}\]. Then the height of the tree (Given \[\sin \,{22^0}\, = \,0.3746,\]\[\cos \,{22^0}\, = \,0.9276\]from tables) is
A. 18.4 m
B. 20.4 m
C. 18.54 m
D. 30 m

Answer 1

Hint: The first and probably the most common use of trigonometry in the real world is the measuring of the height of a building or any other structure standing tall and it is to be done with the help of trigonometric ratios.
Trigonometric ratios are applicable only in a right angle triangle.
A right angle triangle includes a hypotenuse (the longest side), base, & the perpendicular.
Let a right angle triangle in \[\vartriangle \]ABC

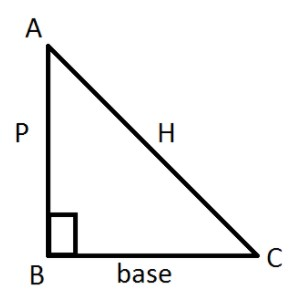
AB \[ = \] P, BC \[ = \] B, and AC \[ = \] H
Where P \[ = \] Perpendicular.
              B \[ = \] Base.
              H \[ = \] Hypotenuse.
Here, \[\sin \theta = \dfrac{P}{H}\], \[\tan \theta = \dfrac{P}{B}\], \[\cos \theta = \dfrac{B}{H}\]
\[\cos ec\,\theta = \dfrac{H}{P}\], \[\cot \,\theta = \dfrac{B}{P}\], \[\sec \,\theta \, = \,\dfrac{H}{B}\].

Complete step by step solution:
Given,
\[\sin \,{22^0} = 0.3746\], \[\cos \,{22^0} = 0.9276\]
Angle of elevation \[ = {45^0}\].
Let PQ be tree and A be the point on the ground AB:

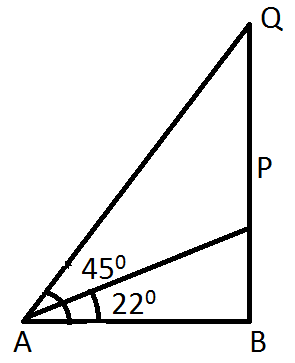
The tree PQ makes an angle of \[{22^0}\]with the horizontal AB
Hence, from A to P i.e. AP \[ = \,35\]m because it is the distance directly down the hill from the base of the tree.
Now, \[\angle QAB = {45^0}\]_____(1), and \[\angle PAB = {22^0}\]
\[ \Rightarrow \angle PAQ = \angle QAB - \angle PAB\]
\[ \Rightarrow \angle PAB = {45^0} - {22^0}\]
\[ \Rightarrow \angle PAQ = {23^0}\]
\[ \Rightarrow \angle AQP = {90^0} - \angle QAB\]
\[ = {90^0} - {45^0} = {45^0}\] [From equation (1)].
Using sine rule in \[\vartriangle QAP\] and \[\vartriangle APB\] we get,
\[\dfrac{{AP}}{{\sin \,{{45}^0}}} = \dfrac{{PQ}}{{\sin \,{{23}^0}}}\]
\[\dfrac{{35}}{{\dfrac{1}{{\sqrt 2 }}}} = \dfrac{{PQ}}{{\sin \,{{23}^0}}}\] [\[\sin \,23 \cong \,\sin \,22 = 0.3746\]]
\[\dfrac{{35}}{{0.709}} = \dfrac{{PQ}}{{0.3746}}\]
\[PQ = \dfrac{{35 \times 0.3746}}{{0.709}} = 18.4\]m.

Hence, the height of the tree is \[18.4\]m.

Note: Trigonometry is used to measure the height or a tree. The distance or the height can be measured with trigonometric ratios only.