Question

A tree is broken at a height of \[5\;m\] from the ground and its top touches the ground at a distance of \[12\;m\] from the base of the tree. Find the original height of the tree.

Answer 1

Hint: In this problem, we use the Pythagoras theorem to find the original height of the tree. By solving this problem by using Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.

Complete step-by-step answer:
A right triangle or right-angled triangle is a triangle in which one angle is a right angle. The relation between the sides and angles of a right triangle is the basis for trigonometry. The side opposite the right angle is called the hypotenuse.
In the given problem,
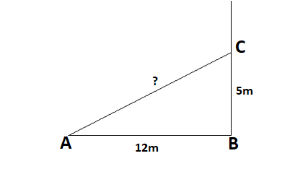
Let \[AB\] be the broken tree top that touches the ground at a distance of \[12\;m\] .
Let \[AC\] be a tree broken at a height of \[5\;m\] .
To find the original height of the tree, \[BC\]
By using Pythagoras theorem, we get
Pythagora's theorem states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.
From the diagram \[\Delta ABC\] are right angled triangles.
In \[\Delta ABC\] , we have
 \[AC{\;^2} = A{B^2} + B{C^2}\]
By substitute the values from the diagram, we get
 \[
  A{C^2} = {12^2} + {5^2} \\
  A{C^2} = 25 + 144 \;
 \]
To simplify, we get
 \[
  A{C^2} = 169 \\
  A{C^2} = {13^2} \;
 \]
Take square root on both sides, then we get
 \[AC = 13\]
Therefore, the value of \[AC = 13\] .
The total height of the tree is \[BC + AC = 5 + 13 = 18\;m\]
Finally, the original height of tree is \[18\;m\]
So, the correct answer is “ \[18\;\;m\] ”.

Note: We have to convert the word problem into mathematical expression by the diagrammatic representation of right angled triangle has three sides are adjacent, opposite and hypotenuse sides. By solving this problem by using Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.