Question

A train travelling at $20\,m{s^{ - 1}}$ accelerates at $0.5\,m{s^{ - 2}}$ for $30\,s$.How far will it travel in this time?

Answer 1

Hint: This question utilizes the concept of mechanics and Newtonian laws of motion. We have all the variables given to us. Using Newton's laws of motion, we can easily deduce the distance travelled by the train in the given time.

Formulae used:
$S = ut + \dfrac{1}{2}a{t^2}$
where $S$ is the distance travelled, $u$ is the initial velocity, $t$ is the time taken to cover distance \[S\] , and $a$ is the acceleration throughout the motion.

Complete step by step answer:
According to the given question, initial velocity with which the train is travelling $u = 20\,m{s^{ - 1}}$. The time period for which the train is travelling $t = 30\,s$. Acceleration of the train during this time period $t$ $a = 0.5\,m{s^{ - 2}}$. The distance travelled by the train during the time period $t$ is $\text{displacement} = S$

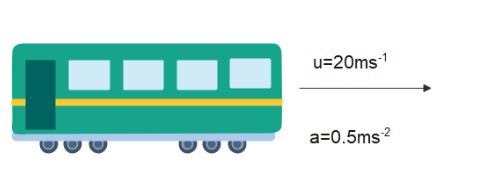
Now using the equation $S = ut + \dfrac{1}{2}a{t^2}$ for the above scenario, we have
$ \Rightarrow S = ut + \dfrac{1}{2}a{t^2}$
Now, substituting the various values in the equation in their respective places, we get
$\Rightarrow S = \left( {20m{s^{ - 1}} \times 30s} \right) + \dfrac{1}{2} \times 0.5m{s^{ - 2}} \times 30s \times 30s \\
\Rightarrow S = 600m + \dfrac{1}{2} \times 450m \\
\Rightarrow S = 600m + 225m \\
\therefore S = 825\,m $

Therefore, the distance travelled by the train during the $30\,s$ , with initial velocity $20\,m{s^{ - 1}}$ and acceleration $0.5\,m{s^{ - 2}}$, is $825\,m$.

Note: We could have also solved the question by first finding the final velocity using the equation $v = u + at$ and then substituting the value of $v$ in the equation ${v^2} - {u^2} = 2aS$ . But that would become lengthy and in competitive exams, time is the most precious asset.