Question

A train travelling at \[{\text{126km/hr}}\] has its speed reduced to \[{\text{54km/hr}}\] while it passes over 500m. Assuming the track is straight and retardation is uniform, find the retardation. How much farther will the train travel before coming to rest?

Answer 1

Hint:In this question, two different speeds of train for two different points are given so, by substituting values of speed in the equation of a uniformly accelerated motion, retardation and distance can be calculated. For calculating distance, final velocity should be considered as 0km/sec.

Complete step by step answer:
Given that, the train initially was travelling at \[{\text{126km/hr}}\]. Thus, let ‘u’ be the initial speed of the train.
\[ {\text{u = 126km/hr}}\]
\[
\Rightarrow {\text{u = }}\dfrac{{{\text{126}} \times {\text{1000}}}}{{60 \times 60}} \\
\Rightarrow {\text{u = 35m/sec}} \\ \]
Now, brakes were applied and the speed of the train was reduced and now its speed is \[{\text{54km/hr}}\]. Meanwhile, the distance covered by train was 500 meter. In more simple words, there was a point A, when speed of train was \[{\text{126km/hr}}\] and then there is a point B where speed of train is \[{\text{54km/hr}}\] and distance between A&B is 500 meter. We are also told that retardation is uniform. Basically, retardation is called negative acceleration or it may be defined as rate of decrease of speed of object.

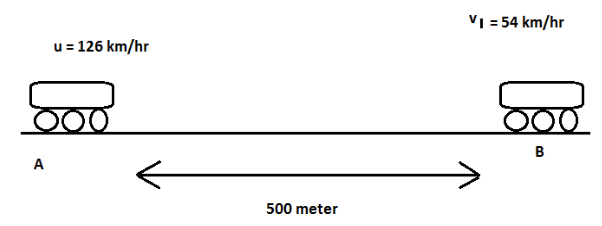
So, let \[{{\text{v}}_1}\]be the speed of the train after applying brakes.
\[{{\text{v}}_1} = 54{\text{km/hr}}\]
\[
\Rightarrow {{\text{v}}_1} = \dfrac{{54 \times 1000}}{{60 \times 60}} \\
\Rightarrow {{\text{v}}_1} = 15m/\sec \\ \]
And ‘S’ be the distance travelled by train between point A and B after retardation.
\[ \Rightarrow {\text{S = 500m}}\]
So, firstly we need to calculate retardation. So, to find that we would use one of the equation of a uniformly accelerated motion, which is:
\[{v^2} - {u^2} = 2as\]…………………..Eq.1
Where, \[u\]= initial velocity of object
\[v\]= final velocity of object
a= acceleration
s = distance travelled
Substitute values in Eq.1 we get,
\[
{v_1}^2 - {u^2} = 2aS
\Rightarrow {(15)^2} - {(35)^2} = 2 \times a \times (500) \\
\Rightarrow 225 - 1225 = a \times 1000 \\
\Rightarrow a = - 1m/{\sec ^2} \\ \]
Thus, retardation of trains is at the rate of\[ - 1m/{\sec ^2}\]. Negative sign of acceleration here represents the decreasing rate of speed of the train.

In the second part of the question, we are asked to find the distance travelled by train before it comes to rest. So, when brakes are applied, the speed of the train starts to decrease at a uniform rate from 126km/hour to 54km/hour and then the train finally comes to rest. Thus, the final speed of the train will be 0km/hour or 0m/sec.Let \[{{\text{v}}_2}\] be the final speed of the train.
\[ {{\text{v}}_2} = 0m/\sec \]
Total distance would be the sum of distance travelled when train comes from 126km/hour to 54km/hour and distance covered by train after 54 km/hour to finally come to rest.
Let ‘x’ be the distance covered by train after 54 km/hour to 0 km/ hour.
So, total distance travelled by train = 500 m + x

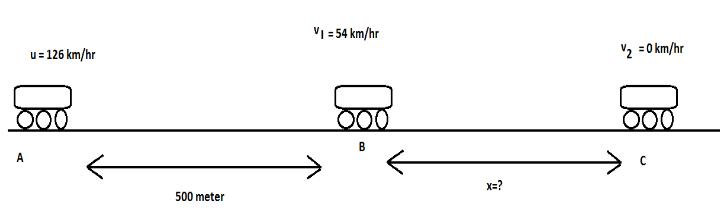
Between point B&C, Consider\[{{\text{v}}_1}\]as initial velocity of train between \[{{\text{v}}_2}\] be the final velocity. Applying, equation of motion:
\[{v^2} - {u^2} = 2as\]
Substituting values in above equation we get:
\[
{v_2}^2 - {v_1}^2 = 2( - 1)x \\
\Rightarrow {0^2} - {(15)^2} = - 2x \\
\Rightarrow - 225 = - 2x \\
\Rightarrow \dfrac{{225}}{2} = x \\
\therefore x = 112.5 \\ \]
Distance covered by train after 54 km/hour to finally come to rest is 112.5 meter. And the total distance covered by train = \[500 + 112.5\]= 612.5 meter.

Distance covered by train is 612.5 meter.

Note: Some minor points to remember:
-All the numerical values of physical quantities like distance, speed, acceleration/retardation used should be in the same unit.
-Retardation was at uniform rate so value of between point B&C would also be equal to -1m/sec.
-Relation used above \[{v^2} - {u^2} = 2as\] is also known as position-Velocity/displacement relation.