Question

A train of mass m moves with a velocity v on the equator from east to west. If $\omega $ is the angular speed of earth about its axis and R is the radius of the earth then the normal reaction acting on the train is
A) $mg\left[ {1 - \dfrac{{\left( {\omega R - 2v} \right)\omega }}{g} - \dfrac{{{v^2}}}{{Rg}}} \right]$
B) $mg\left[ {1 - 2\dfrac{{\left( {\omega R - 2v} \right)\omega }}{g} - \dfrac{{{v^2}}}{{Rg}}} \right]$
C) $mg\left[ {1 - \dfrac{{\left( {\omega R + 2v} \right)\omega }}{g} - \dfrac{{{v^2}}}{{Rg}}} \right]$
D) $mg\left[ {1 - 2\dfrac{{\left( {\omega R + 2v} \right)\omega }}{g} - \dfrac{{{v^2}}}{{Rg}}} \right]$

Answer 1

Hint: When the two surfaces are in contact, the normal reaction acts in perpendicular direction where it is opposite in direction to the weight of the object but equal in magnitude.
The relationship between angular [$\omega $] (in rotation) and linear [v] (in line) velocity is given as:
v = $\omega R$
The earth always rotates from West to east

Complete step by step answer:
Mass of train = m
Velocity of train = v
Weight of the train = mg
Direction of train = east to west
Angular speed of the earth = $\omega $
Radius of the earth = R
Relationship of with linear velocity = $\omega R$
Direction of the earth = west to east
This can be represented through a diagram as:

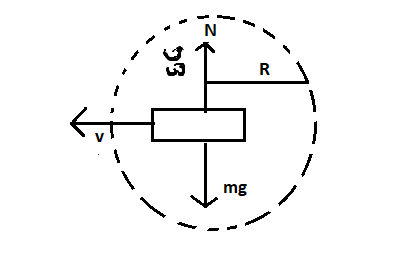
The normal reaction is represented by N which is equal in magnitude of the weight (mg) of the train but opposite in direction.
Now effective velocity can be given as:
${v_{eff}} = v - \omega r$ [As both the velocities are opposite in direction] ________ (1)
The force acting on the train is:
mg – N
This force provides the centripetal force, therefore:
mg – N = $\dfrac{{m{v^2}_{eff}}}{R}$ [ $\because \dfrac{{m{v^2}}}{R}$= centripetal force]
Substituting the value of ${v_{eff}}$ from (1) :
mg – N = $\dfrac{{m{{\left( {v - \omega R} \right)}^2}}}{R}$
$N = mg - \dfrac{m}{R}\left( {{v^2} + {\omega ^2}{R^2} - 2\omega vR} \right)$ \[\left[ {\because \left( {{a^2} + {b^2}} \right) = {a^2} + {b^2} + 2ab} \right]\]
Taking mg common, we get:
$N = mg\left[ {1 - \dfrac{1}{{Rg}}\left( {{v^2} + {\omega ^2}{R^2} - 2\omega vR} \right)} \right]$
Rearranging:
$N = mg\left[ {1 - \dfrac{{\omega R}}{{Rg}}\left( {\omega R - 2v} \right) + \dfrac{{{v^2}}}{{Rg}}} \right]$
$N = mg\left[ {1 - \dfrac{{\left( {\omega R - 2v} \right)\omega }}{g} - \dfrac{{{v^2}}}{{Rg}}} \right]$
Therefore, the normal reaction acting on the given train is $mg\left[ {1 - \dfrac{{\left( {\omega R - 2v} \right)\omega }}{g} - \dfrac{{{v^2}}}{{Rg}}} \right]$ , option A).

Note:The weight was taken as mg because:
It is a force which is acting in the downward direction, so according to Newton’s second law of motion
F = ma but here the body is under the influence of gravity so the acceleration will be the acceleration due to gravity (g).
🡪F = W = mg
The direction of rotation of the earth can be remembered as ‘WE’ – from west to east.