Question

A train of length 50 m is moving with a constant speed of 10 m/s. Find the time taken by the train to cross an electric pole and a bridge of length 250 m.
A) 5 sec and 25 sec
B) 5 sec and 30 sec
C) 5 sec and 45 sec
D) 5 sec and 15 sec

Answer 1

Hint: The distance traveled by train as it crosses the electric pole will be equal to the length of the train. Also, the train must travel a distance equal to the length of the train plus the length of the bridge to cross the bridge.

Formula used:
The time taken $t$ by a body, moving at a speed $s$ to cover a distance $d$ is given by, $t = \dfrac{d}{s}$.

Complete step by step answer:
Step 1: Sketch a figure of the train crossing the pole and the bridge. List the given data.

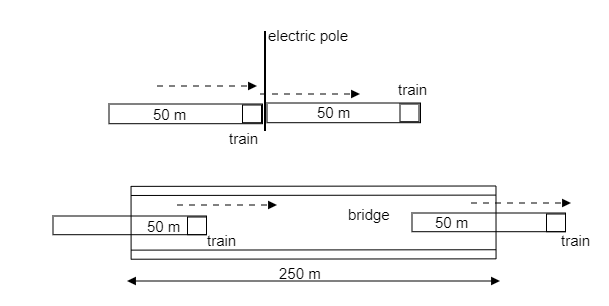
The length of the train is ${l_T} = 50{\text{m}}$. It moves at a constant speed $s = 10{\text{m/s}}$.
The length of the bridge is ${l_B} = 250{\text{m}}$.
Step 2. Find the time taken to cross the electric pole.
The distance covered by the train as it crosses the pole is equal to the length of the train.
i.e., $d = {l_T} = 50{\text{m}}$
Then the time taken to cover this distance is given by, $t = \dfrac{d}{s}$
Substituting the values for $s = 10{\text{m/s}}$ and $d = 50{\text{m}}$ in the above equation we get, $t = \dfrac{{50}}{{10}} = 5{\text{s}}$
So, the time taken to cross the electric pole is 5 sec.
Step 3: Find the distance covered by the train as it crosses the bridge.
As the train crosses the bridge, the train covers a distance equal to its length plus an additional distance equal to the length of the bridge to cross it.
Thus the distance covered by the train to cross the bridge is $d = {l_T} + {l_B}$.
Substituting the values for ${l_T} = 50{\text{m}}$ and ${l_B} = 250{\text{m}}$ in the above equation we get, $d = 50 + 250 = 300{\text{m}}$.
Step 4: Calculate the time taken for the train to cross the bridge.
The speed of the train is $s = 10{\text{m/s}}$ and the distance covered is $d = 300{\text{m}}$.
Then the time taken to cover the distance is given by, $t = \dfrac{d}{s}$
Substituting the values for $s = 10{\text{m/s}}$ and $d = 300{\text{m}}$ in the above equation we get, $t = \dfrac{{300}}{{10}} = 30{\text{s}}$

Therefore, the time is taken by the train to cross the bridge and the pole is 30 sec. Hence the correct option is B.

Note:
A train is said to cross an electric pole when the front of the train to its last wagon crosses it. The length of the electric pole is assumed to be zero but the bridge, however, has a length. This is why the train travels a distance equal to its length to cross the pole but travels an additional length equal to that of the bridge’s to cross the bridge.