Question

A train of length 150m takes 10secs to cross another train 100m long coming from the opposite direction. If the speed of the first train is 30km/hr what is the speed of the second train?
A. 72km/hr
B. 60km/hr
C. 54km/hr
D. 48km/hr

Answer 1

Hint: We will start by using a fact that speed of object A with request to another object B is ${{V}_{A}}-{{V}_{B}}$. Then we will use the fact that $\text{speed =}\dfrac{\text{distance}}{\text{time}}$ to find the speed of the second train.

Complete step-by-step answer:
Now, we have been given that the train of length 150m takes 10secs to cross another train of length 100m coming from the opposite direction.
Now, we let the speed of the second train be $xm/\sec $. Also, we have been given that the speed of the first train is 30km/hr. Now, we know how to convert it in m/sec. we multiply km/hr by $\dfrac{5}{18}$. So, the speed of the first train is $30\times \dfrac{5}{18}m/\sec =\dfrac{25}{3}m/\sec $.

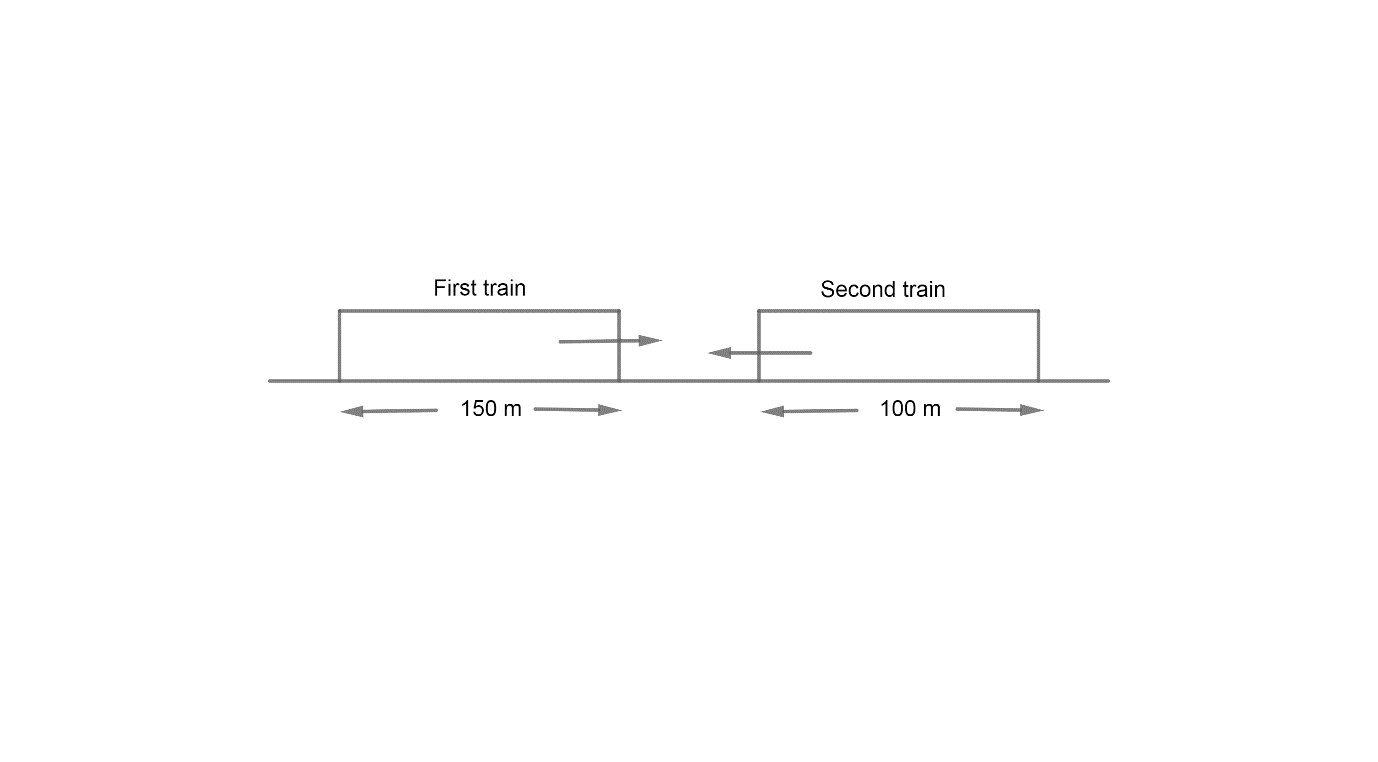
Now, we know that the speed of first train with respect to second train is,
\[{{V}_{f}}-\left( -{{V}_{s}} \right)=\dfrac{25}{3}-\left( -x \right)=\left( \dfrac{25}{3}+x \right)m/s\]
Now, we know that for a train to cross another train it has to cover a distance equal to the speed of both trains as in relative velocity. We have the first train moving with speed \[\left( \dfrac{25}{3}+x \right)m/s\] towards the second train.
Now, we know that $\text{speed =}\dfrac{\text{distance}}{\text{time}}$
$\begin{align}
  & \Rightarrow \dfrac{25}{3}+x=\dfrac{100+150}{10} \\
 & \Rightarrow \dfrac{25}{3}+x=\dfrac{250}{10} \\
 & \Rightarrow \dfrac{25}{3}+x=25 \\
 & \Rightarrow x=25-\dfrac{25}{3} \\
 & \Rightarrow x=\dfrac{50}{3}m/\sec \\
\end{align}$
Now, we have to convert x in km/hr. For this we multiply it by $\dfrac{18}{5}$. So, we have,
$\begin{align}
  & x=\dfrac{50}{3}\times \dfrac{18}{5}km/hr \\
 & =60km/hr \\
\end{align}$

So, the correct answer is “Option B”.

Note: It is important to note that in the relative frame we have the second train as stationary and first train moving with speed \[\dfrac{25}{3}+x\]. Also, it is important to remember to convert km/hr to m/sec. We multiply by factor \[\dfrac{5}{18}\] this makes the solution easier.