Question

A train has to negotiate a curve of radius $400\,m$. By how much should the outer rail be raised with respect to the inner rail for a speed of $48\,kmph$. The distance between the rails is $1\,m$
A. $12\,m$
B. $12\,cm$
C. $4.5\,cm$
D. $4.5\,m$

Answer 1

Hint:This question utilizes the concept of banking of roads. Here, the railway tracks are banked to prevent slipping of the train from its tracks. We can use the formula of banking of roads here with a few modifications and find out the answer.

Formulae used:
$\tan \theta = \dfrac{{{v^2}}}{{rg}}$
where $\theta $ is the angle of inclination, $r$ is the radius of the curve to be negotiated, $g$ is the acceleration due to gravity and $v$ is the velocity of the car/train.
$\tan \theta = \dfrac{h}{b}$
where $h$ is the height of the right angled triangle and $b$ is the base
Useful conversions:
$1\,kmph = \dfrac{5}{{18}}\,m{s^{ - 1}}$

Complete step by step answer:
According to the given question
Radius of the curve $r = 400\,m$
Velocity of the train $v = 48\,kmph$
Converting to SI unit, we have,
$v = 48 \times \dfrac{5}{{18}}\,m{s^{ - 1}} \\
\Rightarrow v= \dfrac{{40}}{3}\,m{s^{ - 1}}$
Acceleration due to gravity $g = 9.8\,m{s^{ - 1}}$

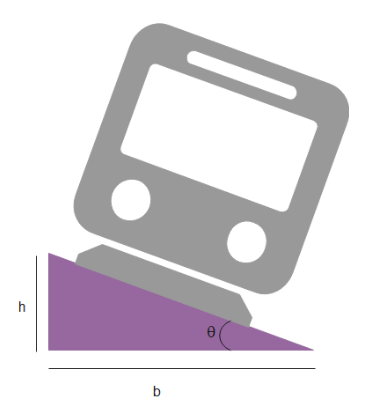
Applying $\tan \theta = \dfrac{h}{b}$ here, where $h$ is the elevation of the outer rail from the inner one and the distance between two rails is given as $b = 1m$
We have
$\tan \theta = \dfrac{h}{1}$ ----(i)
Also we know
$\tan \theta = \dfrac{{{v^2}}}{{rg}}$ -----(ii)
Merging eq (i) and (ii) , we have
$\Rightarrow \dfrac{{{v^2}}}{{rg}} = \dfrac{h}{{1m}} \\$
Substituting the respective values, we have
$ \Rightarrow \dfrac{{{{\left( {\dfrac{{40}}{3}m{s^{ - 1}}} \right)}^2}}}{{400m \times 9.8m{s^{ - 2}}}} = \dfrac{h}{{1m}}$
$\Rightarrow h = 0.0045m \\
\therefore h = 4.5\,cm $

Thus, the correct answer is option C.

Note:Normally, this track can take the above velocity with ease in this situation. But in real life scenarios, the velocity can be increased even more because friction comes into play. Also, tracks are made to withstand about $3$ to $4$ times more than the maximum velocity to prevent any accident.