Question

A train approaching a railway crossing at a speed of $180km{h^{ - 1}}$sounds a short whistle at a frequency $600Hz$, when it is $400m$ away from crossing. The speed of sound in air is $340m{s^{ - 1}}$. The frequency of the sound heard by a person standing on a road perpendicular to a track at a distance of $300m$ from the crossing is:

A. $680Hz$
B. $480Hz$
C. $40Hz$
D. $50Hz$

Answer 1

Hint:
Hint-Frequency of the sound depends on the distance. Because we know the sound waves lose energy while travelling long distances.

Formula used:
$n' = n\left[ {\dfrac{V}{{V - {V_s}\cos \theta }}} \right]$
Where,
$n'$=frequency of the whistle sound heard by the person standing on a road.
$n$=frequency of the whistle sound produced by the train.
\[V\]=velocity of the sound in air
\[{V_s}\]=velocity of the train
\[\theta \]=angle between the train and the road which are perpendicularly connected.

Complete step by step answer:
The velocity of the train, \[{V_s} = 180km{h^{ - 1}}\]. We should convert this velocity in metres and seconds.
\[ \Rightarrow {V_s} = \dfrac{{180 \times {{10}^3}}}{{3600}}\]
\[\therefore {V_s} = 50m{s^{ - 1}}\]
The velocity of sound in air, \[V = 340m{s^{ - 1}}\]
The frequency of sound produced by train, \[n = 600Hz\]
Now we need to find the angle between the track and road. For that we should know the perpendicular distance. We have an imaginary diagram for that.

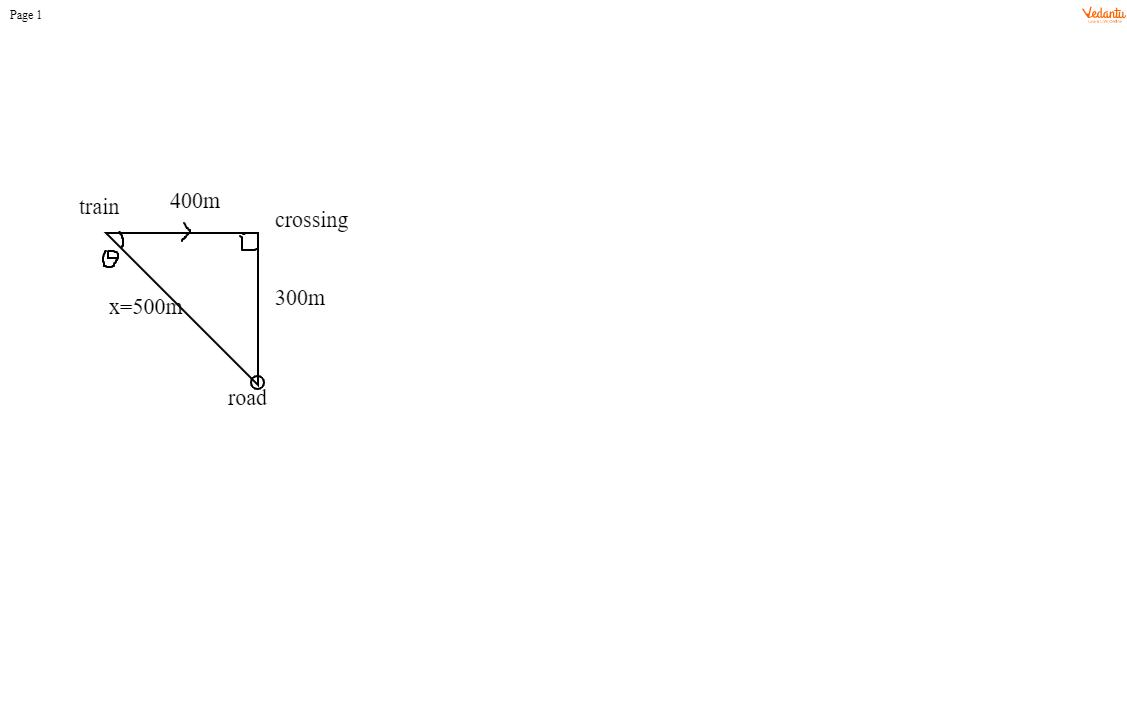
From this diagram, we can find the perpendicular distance, $x$ between the track and road by Pythagoras theorem.
 \[x = \sqrt {{{\left( {300} \right)}^2} + {{\left( {400} \right)}^2}} \]
\[ \Rightarrow x = 500m\]
We want to know the angle between the train and the road. Hence we use cosine formula.
\[\cos \theta = \dfrac{{400}}{{500}}\]
\[ \Rightarrow \cos \theta = \dfrac{4}{5}\]
Now we apply all the values we know in the formula,
$n' = n\left[ {\dfrac{V}{{V - {V_s}\cos \theta }}} \right]$
\[n' = 600\left[ {\dfrac{{340}}{{340 - 50 \times \dfrac{4}{5}}}} \right]\]
\[n' = 600\left[ {\dfrac{{340}}{{340 - 40}}} \right]\]
\[n' = 600\left[ {\dfrac{{340}}{{300}}} \right]\]
\[n' = 2\left[ {340} \right]\]
\[n' = 680Hz\]
Therefore, the frequency of the sound heard by the person in the road is \[680Hz\].

So, the correct answer is “Option A”.

Additional Information:
(i)When the sound waves travel a lot it loses its energy. Here, the sound reaches the person in the road with high frequency because the road is parallel to the train’s direction.
(ii)We hear the sound of the vehicle which is in the same direction of us fastest and with more frequency than the one coming from the opposite.

Note:
The sound waves lose their energy while travelling long distances. The vibration or the speed of the sound that determines the pitch of the sound is known as frequency. It can be calculated as the number of wave cycles that occur in one second and it is measured in hertz.