Question

A train approaches a tunnel AB. Inside the tunnel is a cat located at a point that is $\dfrac{3}{8}$ of the distance AB measured from the entrance A. When the train whistles, the cat runs. If the cat moves to the entrance of tunnel A, the train catches the cat exactly at the entrance. If the cat moves to the exit B, the train catches the cat exactly at the exit. The speed of the train is greater than the speed of the cat by what order?
(A). $3:1$
(B). $4:1$
(C). $5:1$
(D). None of these

Answer 1

Hint – To solve this question, first we have to form an imaginary image in our minds, and then draw it to make it easy to understand the question. Then, by using the formulas, we will be framing the equations for two cases (based on cat’s movement) and by further calculations, we will approach our Solution.

Complete step-by-step solution -

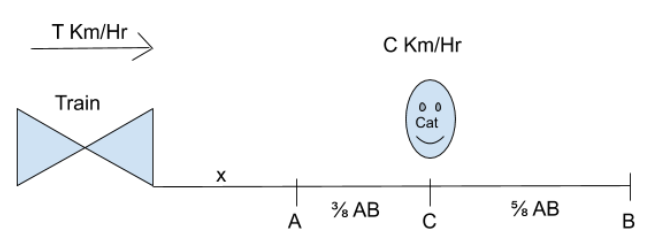
Let Distance between Train and Entrance of Tunnel when the Train Whistles be $x$ and length of tunnel be AB
Let the speed of the Train and Cat be T km/hr. and C km/hr. respectively.
 Here $\dfrac{3}{8} \times AB$ is the distance covered by cat and C is the speed of cat while moving towards A which calculates the time taken by cat to reach A. It will be equal to the time taken by train to reach A as the train and cat meet at A and x is the distance covered by the train and T is the speed of the train.
Similarly when the train is moving towards B ,it will cover $x + AB$ distance at the speed of T km/hr which will calculate time which will be equal to time taken by cat while covering $\dfrac{5}{8} \times AB$ distance at the speed of C km/hr.

When the cat moves Towards the Entrance A,
$ \Rightarrow \dfrac{x}{T} = \dfrac{3}{8} \times \dfrac{{AB}}{C}..................\left( 1 \right)$
When the Cat Move Towards the Entrance B,
$ \Rightarrow \dfrac{{x + AB}}{T} = \dfrac{5}{8} \times \dfrac{{AB}}{C}..................\left( 2 \right)$
On Dividing Equation$\left( 1 \right)$ by Equation$\left( 2 \right)$ we get
$
  \dfrac{x}{{x + AB}} = \dfrac{3}{5} \\
    \\
$
$x = \dfrac{{3AB}}{2}$
Putting value of $x$ in Eq$\left( 1 \right)$ we get
$ \Rightarrow \dfrac{{3AB}}{{2T}} = \dfrac{3}{8} \times \dfrac{{AB}}{C}$
$
   \Rightarrow T:C = 4:1 \\
    \\
$
Therefore, the correct answer is option B. $4\,:\,1$.

Note - The speed of train i.e. T km/hr. should not be confused with time as we are using the formula $Time = \,\dfrac{{Dis\tan ce}}{{Speed}}$ for calculating time and then putting the equations together as the time taken by train and cat to reach A and B is same. This information is very helpful to solve this type of question.