Question

A track of uniform path $ 2m $ wide runs around a rectangular park $ 50\,m $ in length and $ 36\,m $ in breadth. Calculate the area of the track.

Answer 1

Hint: For a given question we first find the length breadth of a rectangle formed out of the given rectangular park by adding width of park and then finding the difference of areas of two rectangles so formed to have the required area of path.
Area of rectangle = $ Length(L) \times Breadth(B) $

Complete step-by-step answer:
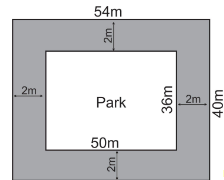
Dimensions of rectangular park are $ 50\,m $ by $ 36\,m $ .
Therefore, we say that the length of the rectangular park is $ 50\,m $ and the breadth of the park is $ 36\,m $ .
Since, it is given that there is a path of $ 2m $ width runs around the rectangular park.
Which implies that there is another big rectangle which is outside the given rectangular park.
Dimension of a big rectangle can be calculated by adding $ 4 $ to both the length and breadth of the given rectangle.
Therefore, Length of big rectangle = $ 50 + 4 = 54\,m $
Breadth of big rectangle = $ 36 + 4 = 40\,m $

Now, to find the area of the path which is in between two rectangles can be calculated by calculating the difference of areas of two rectangles.
For this we first calculate the area of the big rectangle which is given as a product of length and breadth.
 $ \therefore $ Area of big rectangle = $ 54 \times 40 = 2160 $
Hence, area of big rectangle is $ 2160\,{m^2} $
Now, we calculate the area of a small rectangle which is given as a product of length and breadth.
 $ \therefore $ Area of small rectangle = $ 50 \times 36 = 1800 $
Hence, are of small rectangle is $ 1800\,{m^2} $
Now, for the area of the path we calculate the difference of the areas of rectangles above calculated.
Therefore area of path = Area of big rectangle – area of small rectangle.
Area of path = $ 2160 - 1800 $
Area of path = $ 360\, $
From above we see that the Area of path that runs around a given rectangular park is $ 360\,{m^2} $ .

Note: While finding a solution for this type of problem students go through the statement very carefully and then decide whether the path is either out the given rectangular park or inside the given rectangular park. As, for outside we find length and breadth by adding width of the park to given length and breadth and for inside we calculate length and breadth after subtracting to given length and breadth.