
A toy train consists of three identical compartments X,Y and Z. It is pulled by a constant horizontal force F applied on Z horizontally. Assuming there is negligible friction, the ratio of tension in string connecting XY and YZ is:
A. 2:1
B. 3:2
C. 1:2
D. 2:3
Answer
578.4k+ views
Hint: Apply Newton’s second law to the compartment Z to determine the tension in compartment Y and Z. Then apply the same for compartment Y to determine the tension between compartment X and Y.
Complete step by step answer:
We assume the mass of each compartment is m and acceleration is a. We can draw of the forces acting on each compartment of the toy train as follows,
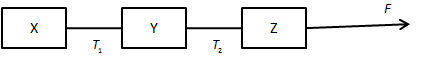
In the above figure, \[{T_1}\] is the tension in the string connecting the compartments X and Y, \[{T_2}\] is the tension in the string connecting the compartments Y and Z.
Now, we can see, the total mass of the toy train is 3m. Therefore, if we apply Newton’s second law in the horizontal direction, we get,
\[F = 3ma\]
Therefore, the acceleration in each compartment is,
\[a = \dfrac{F}{{3m}}\]
Now, we apply Newton’s second law of motion to the motion of compartment Z as follows,
\[F - {T_2} = ma\]
\[ \Rightarrow {T_2} = F - ma\]
Substitute \[F = 3ma\] in the above equation.
\[{T_2} = 3ma - ma\]
\[ \Rightarrow {T_2} = 2ma\]
Similarly, we can apply Newton’s second law to the motion of compartment Y as follows,
\[{T_2} - {T_1} = ma\]
\[ \Rightarrow {T_1} = {T_2} - ma\]
Substitute \[{T_2} = 2ma\] in the above equation.
\[{T_1} = 2ma - ma\]
\[ \Rightarrow {T_1} = ma\]
Now, we can take the ratio of \[{T_1}\] and \[{T_2}\].
\[\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{ma}}{{2ma}}\]
\[ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{1}{2}\]
\[ \Rightarrow {T_1}:{T_2} = 1:2\]
So, the correct answer is “Option C”.
Note:
While applying Newton's second law of motion to the body which is acted upon by more than one force, the direction of force is important to determine the net force. In the solution, we have considered the force towards the right to be positive and force towards the left be negative.
Complete step by step answer:
We assume the mass of each compartment is m and acceleration is a. We can draw of the forces acting on each compartment of the toy train as follows,
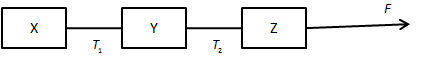
In the above figure, \[{T_1}\] is the tension in the string connecting the compartments X and Y, \[{T_2}\] is the tension in the string connecting the compartments Y and Z.
Now, we can see, the total mass of the toy train is 3m. Therefore, if we apply Newton’s second law in the horizontal direction, we get,
\[F = 3ma\]
Therefore, the acceleration in each compartment is,
\[a = \dfrac{F}{{3m}}\]
Now, we apply Newton’s second law of motion to the motion of compartment Z as follows,
\[F - {T_2} = ma\]
\[ \Rightarrow {T_2} = F - ma\]
Substitute \[F = 3ma\] in the above equation.
\[{T_2} = 3ma - ma\]
\[ \Rightarrow {T_2} = 2ma\]
Similarly, we can apply Newton’s second law to the motion of compartment Y as follows,
\[{T_2} - {T_1} = ma\]
\[ \Rightarrow {T_1} = {T_2} - ma\]
Substitute \[{T_2} = 2ma\] in the above equation.
\[{T_1} = 2ma - ma\]
\[ \Rightarrow {T_1} = ma\]
Now, we can take the ratio of \[{T_1}\] and \[{T_2}\].
\[\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{ma}}{{2ma}}\]
\[ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{1}{2}\]
\[ \Rightarrow {T_1}:{T_2} = 1:2\]
So, the correct answer is “Option C”.
Note:
While applying Newton's second law of motion to the body which is acted upon by more than one force, the direction of force is important to determine the net force. In the solution, we have considered the force towards the right to be positive and force towards the left be negative.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




