Question

A toy is in the form of a cone of radius $r$ cm mounted on a hemisphere of the same radius. The total height of the toy is $\left( r+h \right)$ cm. then the volume of the toy is

Answer 1

Hint: In this problem we need to calculate the volume of the toy according to its shape. Given that the toy is in the form of a cone of radius $r$ cm mounted on a hemisphere of same radius. The total height of the toy is $\left( r+h \right)$ cm. So, we will first represent this data in the diagrammatic form. Now we will consider the toy as two shapes which are sphere and cone. Now we will calculate the volume of each shape individually and sum them to get the required result.

Complete step by step solution:
Given that the toy is in the form of a cone of radius $r$ cm mounted on a hemisphere of same radius. The total height of the toy is $\left( r+h \right)$ cm. The diagram of the cone is given by

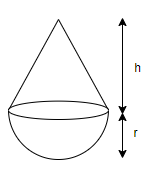
In the above diagram we can observe two shapes which are cone having radius $r$ cm, height $h$ cm and a semi sphere of radius $r$ cm.
Now considering the cone shape having radius $r$ cm, height $h$.
We know that the volume of the cone having radius $r$ cm, height $h$ is given by
${{V}_{cone}}=\dfrac{1}{3}\pi {{r}^{2}}h$.
Now considering the semi sphere shape of radius $r$cm.
We know that the volume of the hemisphere of radius $r$cm is given by
${{V}_{sphere}}=\dfrac{2}{3}\pi {{r}^{3}}$.
Now the total volume of the toy is the sum of the volumes of cone and hemisphere, then we will get
$\begin{align}
  & {{V}_{toy}}={{V}_{cone}}+{{V}_{sphere}} \\
 & \Rightarrow {{V}_{toy}}=\dfrac{1}{3}\pi {{r}^{2}}h+\dfrac{2}{3}\pi {{r}^{3}} \\
\end{align}$
Taking the term $\dfrac{\pi }{3}{{r}^{2}}$ as common from the above equation, then we will have
${{V}_{toy}}=\dfrac{\pi }{3}{{r}^{2}}\left( h+2r \right)$.

Hence the total volume of the toy is $\dfrac{\pi }{3}{{r}^{2}}\left( h+2r \right)$.

Note: In this problem they have directly asked to calculate the volume of the toy. Sometimes they may ask to calculate the paper required to make the toy or the money required to paint the toy, then we need to calculate the total surface area of the cone by using the formulas $S.{{A}_{cone}}=\pi r\left( r+\sqrt{{{r}^{2}}+{{h}^{2}}} \right)$, $S.{{A}_{semi-sphere}}=3\pi {{r}^{2}}$.