Question

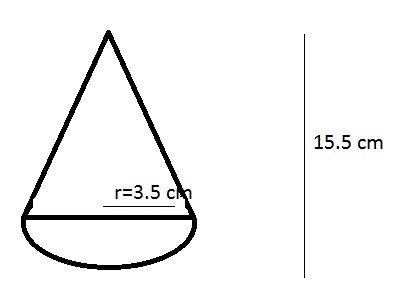
A toy in the form of a cone of radius 3.5 cm mounted on a hemisphere of the same radius. The total height of the toy is 15.5 cm, find the total surface area of the toy.

Answer 1

Hint:
To find the total surface area of the toy we should find the surface area of hemisphere and cone separately and use the following process.
$\text{Total surface area of toy = curved surface area of the hemisphere + curved surface area of the cone.}$

Formula used:
Curved surface area of hemisphere \[ = 2\pi {r^2}\]
Curved surface area of cone \[ = \pi rl\]

Complete step by step answer:
Let us find curved surface area of hemisphere, here it is given that
Radius of hemisphere = radius of cone = $r = 3.5 cm$
We have to find the Curved surface area of the hemisphere. So we use formula of Curved surface area of hemisphere
Curved surface area of hemisphere \[ = 2\pi {r^2}\]
Let us substitute the known values,
\[ = 2 \times \dfrac{{22}}{7} \times {\left( {3.5} \right)^2}\]
On solving the above equation we get,
\[ = 2 \times \dfrac{{22}}{7} \times 3.5 \times 3.5\]
\[ = 2 \times 22 \times 0.5 \times 3.5\]
Area of the hemisphere \[ = {\rm{ }}77{\rm{ }}c{m^2}\]
Hence curved surface area of hemisphere is \[77{\rm{ }}c{m^2}\]
Now let us find the curved surface area of cone
We know that, Curved surface area of cone \[ = \pi rl\]
Here it is given that
Radius of cone $= r =$ \[3.5{\rm{ }}cm\]
We have to find the height of cone, as we know that
$\text{Height of cone = total height of toy - radius of hemisphere}$
Height of cone \[ = 15.5 - 3.5\]
Height of cone \[ = 12{\rm{ }}cm\]
Using the height and radius we find the slant height with the help of the following formula,
Slant height of cone is \[{l^2} = {h^2} + {r^2}\]
Let us now substitute the known values we get,
$\Rightarrow$ \[{l^2} = {\left( {12} \right)^2} + {\left( {3.5} \right)^2}\]
By finding the square values in the equation we get,
$\Rightarrow$ \[{l^2} = 144 + 12.25\]
Let us add the terms and take square root on both sides we get,
$\Rightarrow$ \[{l^2} = 156.25\]
$\Rightarrow$ \[l = \sqrt {156.25} = 12.5{\rm{ }}cm\]
On solving we have found that the slant height of cone is 12.5 cm
We have to find Curved surface area of cone, we know that
Curved surface area of cone \[ = \pi rl\]
Let us substitute the known values we get,
$\Rightarrow$ \[ \dfrac{{22}}{7} \times 3.5 \times 12.5\]
Let us solve the above equation further we get,
$\Rightarrow$ \[ 22 \times 0.5 \times 12.5\]
$\Rightarrow$Area of the cone \[ = 137.5{\rm{ }}c{m^2}\]
$\Rightarrow$ The curved surface area of cone is \[137.5{\rm{ }}c{m^2}\]
Now,
We have to find the total surface of the toy, we know that
$\text{Total surface area of toy = curved surface area of hemisphere + curved surface area of cone}$
By substituting the known values we get,
$\Rightarrow$ Total surface area of toy \[ = 77 + 137.5\]
\[ = 214.5{\rm{ }}c{m^2}\]

$\therefore$ The total surface area of the toy is \[214.5{\rm{ }}c{m^2}\]

Note:
A cone is a 3-dimensional geometry that has a planner circular base associated with a lateral surface. There is a vertex associated with a lateral surface.
The height of the cone is the distance between the vertex and the center of the base.