Question

A tower \[{T_1}\] of height 60m is located exactly opposite to a tower \[{T_2}\]of height 80m on a straight road. From the top of \[{T_1}\] , if the angle of depression of the foot of \[{T_2}\] , is twice the angle of elevation of the top of \[{T_1}\], then the width ( in m ) of the road between the feet of the towers \[{T_1}\] and \[{T_2}\] is:
\[A.{\text{ }}10\sqrt 2 \]
\[B.{\text{ }}10\sqrt 3 \]
\[C.20\sqrt 3 \]
\[D.20\sqrt 2 \]

Answer 1

Hint :- We had to assume the distance between the road from the feet of tower ( \[{T_1}\] ) and tower ( \[{T_2}\] ) and then by using the trigonometric formulas such as \[\tan \theta = \dfrac{{{\text{Height}}}}{{{\text{Base}}}}\] and \[\cot \theta = \dfrac{1}{{\tan \theta }} = \dfrac{{{\text{Base}}}}{{{\text{Height}}}}\]. Then after solving these equations we will get the distance of cars from the tower.

Complete step by step solution:
Let us assume that the distance between the road from the feet of tower( \[{T_1}\] ) and tower ( \[{T_2}\] ) is equal to x metres.
Now let us assume that the angle of elevation from top of \[{T_1}\] is \[\theta \].
So, according to the question , the angle of the depression of the foot of \[{T_2}\] must be \[2\theta \].
Now let us understand this all with the help of a diagram that is given below

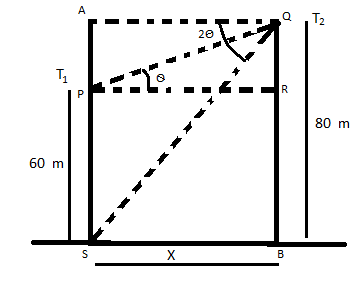
So, now according to the diagram we can say \[\angle QPR = \theta \]and \[\angle AQS = 2\theta \].
Now as we know that \[\tan \theta = \dfrac{{perpendicular}}{{base}}\].
So, applying \[\tan \theta \] in \[\Delta QPR\]
\[ \Rightarrow \tan \theta = \dfrac{{perpendicular}}{{base}} = \dfrac{{QR}}{{PR}}\]
And now QR = QB – RB and PR = SB so can say that QR = 80 – 60 = 20 and PR = x
\[ \Rightarrow \tan \theta = \dfrac{{20}}{x}\]
Now as we know that in \[\Delta AQS\],\[\theta \] becomes \[2\theta \] so now applying \[\tan 2\theta \] in \[\Delta AQS\]
\[ \Rightarrow \tan 2\theta = \dfrac{{AS}}{{AQ}}\] ( AS = QB and AQ = SB )
\[ \Rightarrow \tan 2\theta = \dfrac{{80}}{x}\]
Now the width of road between the feet of both towers must be equal and we know that \[\tan 2\theta = \dfrac{{2\tan \theta }}{{1 - {{\tan }^2}\theta }}\].
So, using the above identity to solve the question
\[\tan 2\theta = \dfrac{{2\tan \theta }}{{1 - {{\tan }^2}\theta }}\]
\[ \Rightarrow \dfrac{{80}}{x} = \dfrac{{2 \times \dfrac{{20}}{x}}}{{1 - {{\left( {\dfrac{{20}}{x}} \right)}^2}}}\] ( \[\tan 2\theta = \dfrac{{80}}{x}\] and \[\tan \theta = \dfrac{{20}}{x}\] )
Now taking L.C.M of denominator of R.H.S and solving it
\[ \Rightarrow \dfrac{{80}}{x} = \dfrac{{\dfrac{{40}}{x}}}{{\dfrac{{{x^2} - 400}}{{{x^2}}}}}\]
\[ \Rightarrow \dfrac{{80}}{x} = {\text{ }}\dfrac{{40}}{x}{\text{ }} \times {\text{ }}\dfrac{{{x^2}}}{{{x^2} - 400}}\]
Now taking \[\dfrac{{40}}{x}\] common from both L.H.S and R.H.S
\[ \Rightarrow 2 = {\text{ }}\dfrac{{{x^2}}}{{{x^2} - 400}}\]
On cross multiplying we will get
\[ \Rightarrow 2{x^2} - 800 = {x^2}\]
\[ \Rightarrow 2{x^2} - {x^2} = 800\]
\[ \Rightarrow {x^2} = 800{\text{, x}}\,{\text{ = }}\sqrt {800} = 20\sqrt 2 \]
So, the width of roads between the feets of towers is \[20\sqrt 2 \]m
Hence D is the correct option.
Note :- Whenever we come up with this type of problem then we should remember that there is one another way to solve it. i.e. apart from using the trigonometric formula of \[\tan \theta \] we can also use \[\cot \theta \]. And in that case according to the trigonometric formula the values became vice versa .