Question

A tower subtends an angle $ \alpha $ at a point on the same level as the root of the tower and at a second point , b metres above the first, the angle of depression of the foot of the tower is $ \beta $ . The height of the tower is
A. $ b\cot \alpha \tan \beta $
B. $ b\tan \alpha \tan \beta $
C. $ b\tan \alpha \cot \beta $
D. None of these

Answer 1

Hint: As we know that the above given question is a word problem. A problem is a mathematical question written as one sentence or more describing a real life scenario where that problem needs to be solved by the way of mathematical calculation. We can solve the given problem by applying trigonometric ratios formulas.

Complete step-by-step answer:
As per the given question we will draw the diagram and then with the help of that we will mark the angles, draw the triangle and then solve it.

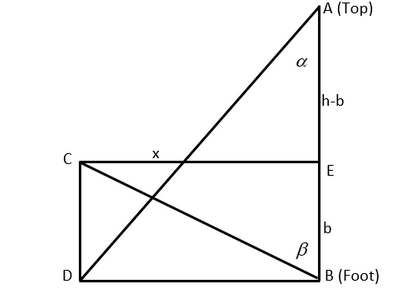
Here in the diagram, we have the following things: ABD is a right angled triangle, $ CE = DB = x $ . BCE is a triangle, right angled triangle. $ AB = h $ and $ EB = b $ , So we can say that $ AE = h - b $ .
We know that
$ \tan \alpha = \dfrac{{height}}{{base}} $ .
In the right angled triangle ABD,
$ \tan \alpha = \dfrac{{height}}{{base}} $ .
Here AB is the height, $ AB = h $ and BD is the base with $ BD = x $ by substituting the values we get:
$ \tan \alpha = \dfrac{{AB}}{{BD}} $ $ \Rightarrow \tan \alpha = \dfrac{h}{x} $ .
So we can write $ h = x\tan \alpha $ .
Now again in the triangle, BCE,
$ \tan \beta = \dfrac{{height}}{{base}} $ ,
in this figure BE is the height and EC is the base. Therefore
$ \tan \beta = \dfrac{{BE}}{{EC}} $ ,
here $ BE = b,EC = x $ . By putting the values in the expression, we have;
$ \tan \beta = \dfrac{b}{x} $ .
We can write $ x = \dfrac{b}{{\tan \beta }} $ .
By putting this value of $ x $ in the first expression we have,
$ h = \dfrac{b}{{\tan \beta }} \times \tan \alpha $ , we know that $ \cot \theta = \dfrac{1}{{\tan \theta }} $ . So we can write $ b\tan \alpha \cot \beta $ .
Hence the correct option is C. $ b\tan \alpha \cot \beta $ .
So, the correct answer is “Option C”.

Note: We should always be careful what the question is asking and we will find it in trigonometric terms. Based on the requirement and by observing all the necessary information that is already available in the question we gather the information and then create an equation or by unitary method whichever is applicable, then we solve the problem and then verify the answer by putting the value in the problem and see whether we get the same answer or not.