Question

A tourist drives 10 km toward east and turns to the right hand and drives 3 km. Then he drives towards the west 3 km. Then he turns to his left and drives 2 km. Finally, he turns to his right and travels 7 km. How, far is he from his starting point and in which direction would he be?
(a) 10 km east
(b) 9 km north
(c) 18 km west
(d) 5 km south

Answer 1

Hint: We start solving the problem by drawing all the given following the directions that were mentioned in the problem. We then calculate the horizontal distances involved from the figure to check the direction of the ending point from the starting point. We then make use of the vertical distances that were involved in the figure to get the resulting distance between starting and ending points. Using the obtained results of distance and direction, we write the final result.

Complete step-by-step answer:
According to the problem, we are given that a tourist drives 10 km towards east and turns to his right hand and drives 3 km. Then, he drives towards the west for 3 kms and turns to his left to drive for 2 km. Finally, he turns to his right and travels 7 km. We need to find the distance that the tourist is away from the starting position.
Let us draw the given and information along with the directions to get a better view.

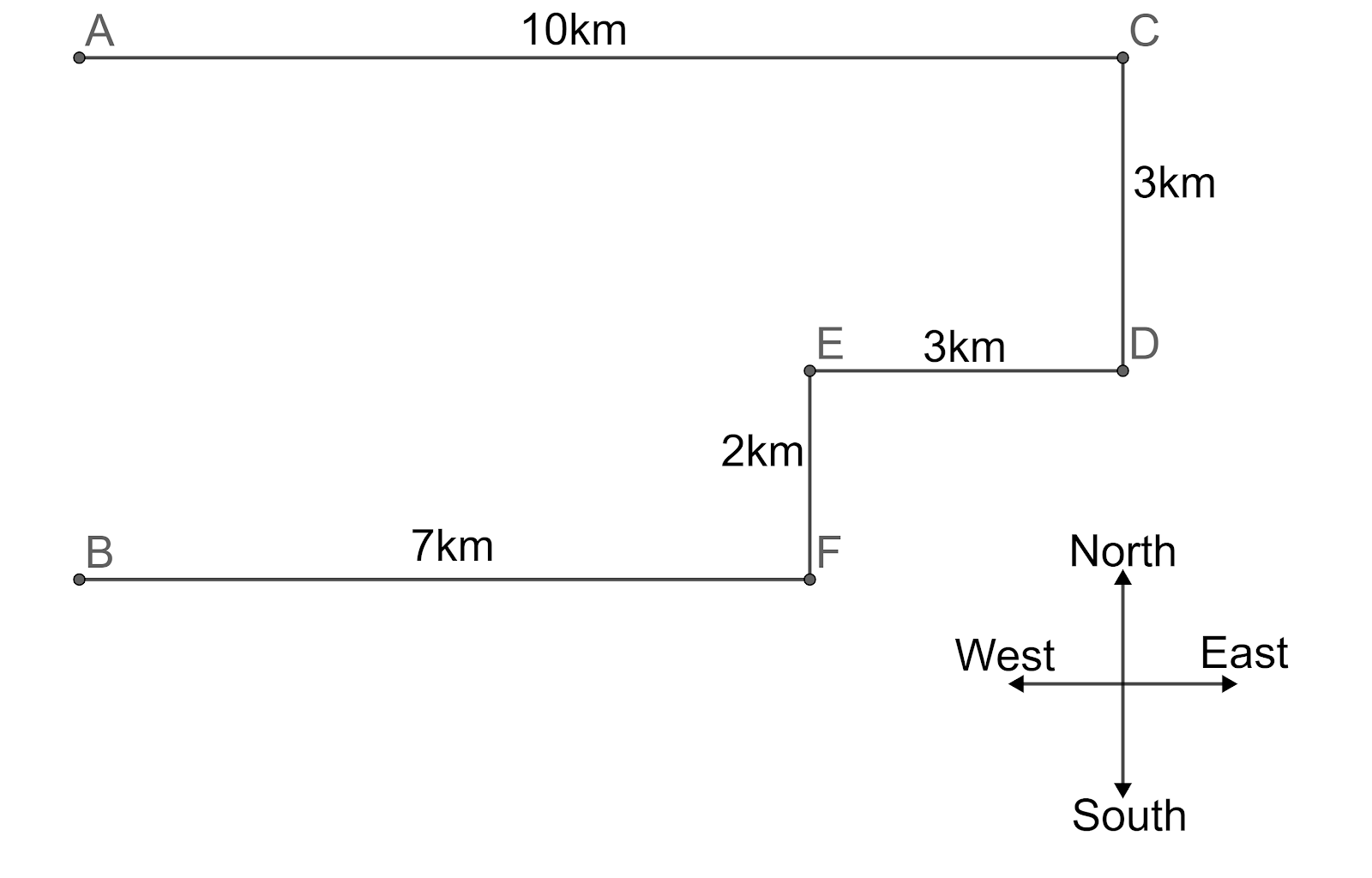
From the diagram We can see that tourists drive 10 km towards the east that is represented by AC. Then he turns to his right side and drives 3 km that is represented by a CD. Then he drives towards the west (turning to his right) that is represented by DE. He then turns to his left side and drives 2 km that is represented by EF. Now, finally turns to his right side and travels 7 km which is represented by FB.
From the figure we can see that ED and BF distance is 3 km and 7 km respectively. This tells us that the tourist travelled horizontally a distance of $\left( 3+7 \right)$ km or 10 km.
Now, we found that the distance of AC is 10 km so is the sum of BF and ED. We can say that A, B are perpendicularly on the same line.
From the figure, we can say that distance between the points A, B can be found by adding the distances of CD and EF which is equal to $3\ km+2\ km$ or 5 km and we can see that the B is south to the point A, which tells us that the tourist is 5km south to the starting point.
∴ The tourist is 5km south to the starting point.

So, the correct answer is “Option d”.

Note: In this problem while drawing the route map, we assumed west as the geographical west as directions are shown beside the route map i.e., right side of the tourist. We can also solve this problem by taking the west of the tourist (i.e., to the left side of the tourist) which may need usage of properties of triangles to get the required value. Whenever we get this type of problem, we should start solving it by drawing the route map as it will give us half of the answer without any calculation.