Question

A toroid has a core (non-ferromagnetic) of inner radius 25cm and outer radius 26cm, around which 3500 turns of a wire are wound. If the current in the wire is 11A, the magnetic field inside the core of the toroid is?

Answer 1

Hint: We’ve been given a toroid whose inner radius is 25cm and the outer radius is 26.5cm, from this we can find the radius of the amperian loop of the toroid. The magnetic field inside the toroid will be given by the ampere’s circuital law, which states that the magnetic field along an imaginary closed path (i.e. amperian loop) is equal to the product of current enclosed by the amperian loop and the permeability of the medium.

Formula used:
$B = \dfrac{{{\mu _0}NI}}{{2\pi R}}$

Complete step-by-step solution:

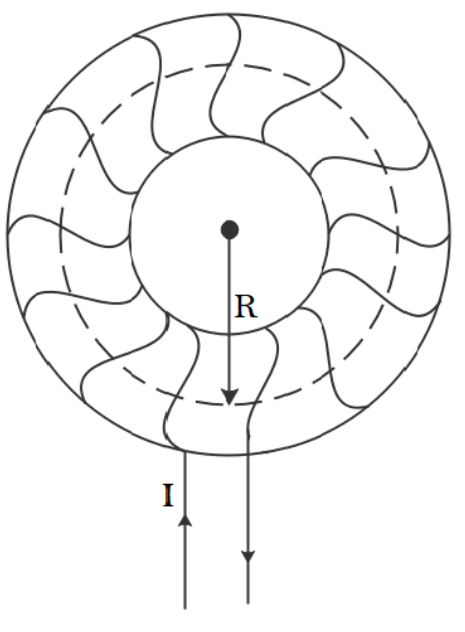
In the problem, they’ve given a toroid of inner radius 25cm and outer radius 26cm. But we will consider the radius of the dotted circle (amperian loop) as the field exists in the core part of the toroid. The radius R will be
$R = \dfrac{{25 + 26}}{2} = 25.5cm$
From Ampere’s circuital law, we have that the relationship between current and the magnetic field as
$B = \dfrac{{{\mu _0}NI}}{{2\pi R}}$
Where,
${\mu _0}$ is the permeability given by $4\pi \times {10^ - }^7N/{A^2}\;$
N is the number of turns
“I” is the current through the coil
R is the radius of the amperian loop
We found the radius of the amperian loop to be $25.5cm$ which can be written as $25.5 \times {10^{ - 2}}m$. They’ve given that the number of turns is 3500 and the current passing through the wire is 11 A. We also have the value of permeability constant. Substituting these values given in the problem we have
$\begin{align}
  & B = \dfrac{{{\mu _0}NI}}{{2\pi R}} \\
 &\Rightarrow B = \dfrac{{4\pi \times {{10}^ - }^7 \times 3500 \times 11\;}}{{2 \times \pi \times 25.5 \times {{10}^{ - 2}}}} \\
  & \Rightarrow B = 0.0302 T = 3\times {10}^{-2}\\
\end{align}$
Therefore, the magnetic field inside the toroid is $3\times {10}^{-2}T$.

Note: The amperian loop is an imaginary loop, used for measuring the magnetic field in a conductor. It’s important to understand that there exists a magnetic field outside the toroid. But we assume it to be zero as they cancel each other out. This can easily be understood by the right-hand thumb rule. If you point the thumb in the direction of the current the curled fingers will give the direction of the magnetic field due to the current. And it is mentioned that the core of toroid is non-ferromagnetic. Thus, we can take the permeability of free space. But if it was a soft iron core, we’ll have to consider the relative permeability.