Question

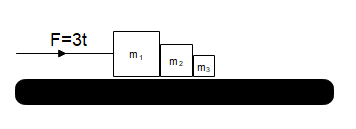
A time-dependent force $ F = 3t\,N $ acts on three blocks $ {m_1},{m_2} $ and $ {m_3} $ kept in contact on rough ground as shown. The coefficient of friction between blocks and ground is $ 0.4 $ . If $ {m_1},{m_2} $ and $ {m_3} $ are 3kg,2kg, and 1kg respectively, the time after which the blocks started to move is $ \left( {g = {\text{ }}10m{s^{ - 2}}} \right) $

A) 4 sec
B) 8 sec
C) $ 8/3 $ sec
D) $ 4/3 $ sec

Answer 1

Hint : The blocks will start to move when the time-dependent force overcomes the static frictional drag force due to the combined frictional force of all three blocks. We will calculate the net frictional force due to three blocks and find the time for which the external force overcomes the frictional force.

Complete step by step answer
We’ve been given that three blocks $ {m_1},{m_2} $ and $ {m_3} $ kept in contact on rough ground as shown and that the coefficient of friction between blocks and ground is $ 0.4 $ .
The net static friction that will act on the three blocks will be the sum of the friction forces of all three blocks. We know that the friction force due to any block can be written as
 $ F = \mu mg $
As the coefficient of friction between the blocks and the surface is $ 0.4 $ , the net friction force which is the sum of friction forces of all the three individual blocks can be written as:
 $ F = 0.4(3)(10) + 0.4(2)(10) + 0.4(1)(10) $
 $ \Rightarrow F = \,24\,N $
Now since the external time-dependent force changes as $ F = 3t\,N $ , we can equalize this force with the total friction force of the three boxes as this will be the time moment where the blocks will start moving. So,
 $ 3t = 24 $
$ \Rightarrow t = 8\,s $ which corresponds to option (B).

Note
Here we have assumed that the blocks stay in contact all the time so that one single block cannot move on its own. While the external force will overcome the individual frictional forces before 8s, the blocks will only start to move when the net friction force will be overcome by the external force.