Question

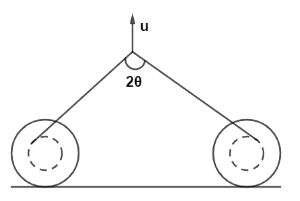
A thread is wounded on two identical bobbins placed on a horizontal floor with their axes parallel. Radius of the outer flanges of bobbins is $\eta $ times that of inner spools. The midpoint of the thread is pulled vertically upwards with a constant velocity $u$ if the bobbins roll on floor without slipping, find velocity of approach of their centers when angle between thread segments becomes $2\theta $. [Take $\theta = 60^\circ ,u = 2m{\sec ^{ - 2}},\eta = \sqrt 3 $ ]

Answer 1

Hint: In order to solve this question we need to understand rolling motion.Rolling motion is a type of motion which combines both rotation and translation of the body with respect to the surface on which this motion is considered. Pure rolling is defined as rolling without translation; this happens only when the rotating frame of reference is at rest or at all points of contact net force is zero. Also rolling without slipping means the point of contact has zero velocity and it translates without being dragged.

Complete step by step answer:
Consider the bobbins rotating with angular velocity $\omega $ and let the outer radius be $R$ and inner radius is $r$.
According to question, $R = \eta r$
Since, $\eta = \sqrt 3 $
So, $R = \sqrt 3 r \to (i)$

Consider the center of bobbins be moving with speed $v$ toward each other as shown,
So velocity of approach of center is given by, ${V_{app}} = v - ( - v)$
${V_{app}} = 2v \to (ii)$
Consider point $1\& 2$ on the string as shown in diagram

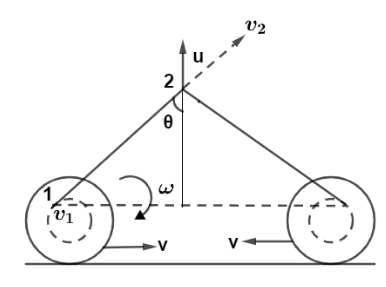
Now for pure rolling we know, $v = R\omega \to (iii)$
Let the velocity at the point where the string is attached with the bobbin be $v'$.Then we know, this point velocity would be along the string and it is equal to,
$v' = \omega r$
So for bobbin there is net velocity as $v'$ and $v$ are two velocities. Let the net velocity at point $1$ along string or toward point $2$ for left bobbin given by ${v_1}$.So from figure,
${v_1} = v' + v\cos (90 - \theta )$
As $v\cos (90 - \theta )$ is a component of center velocity along a string or along point $2$.So,
${v_1} = v' + v\sin (\theta )$

Putting values we get, ${v_1} = \omega r + v\sin \theta \to (iv)$
Also at point $2$ let the velocity be ${v_2}$
So from figure, ${v_2} = u\cos \theta \to (v)$
Since the string is constant, ${v_1} = {v_2}$
So from (iv) and (v) we get,
$u\cos \theta = \omega r + v\sin \theta $
From equation (iii) we get, $\omega = \dfrac{v}{R}$
So, $u\cos \theta = \dfrac{v}{R}r + v\sin \theta $
$u\cos \theta = v(\dfrac{r}{R} + \sin \theta )$
$v = \dfrac{{u\cos \theta }}{{(\dfrac{r}{R} + \sin \theta )}}$

According to question, $\theta = 60^\circ \& R = \eta r$
We get,
$v = \dfrac{{u\cos 60}}{{(\dfrac{r}{{\eta r}} + \sin 60)}}$
$\Rightarrow v = \dfrac{{\dfrac{u}{2}}}{{(\dfrac{1}{\eta } + \dfrac{{\sqrt 3 }}{2})}}$
Using, $\eta = \sqrt 3 $
We get,
$v = \dfrac{{\dfrac{u}{2}}}{{(\dfrac{1}{{\sqrt 3 }} + \dfrac{{\sqrt 3 }}{2})}}$
$\Rightarrow v = \dfrac{{\sqrt 3 u}}{{(1 + 3)}}$
$\Rightarrow v = \dfrac{{\sqrt 3 u}}{4}$
So from (ii) velocity of approach is given by, ${V_{app}} = 2(\dfrac{{\sqrt 3 u}}{4})$
$\therefore {V_{app}} = \dfrac{{\sqrt 3 u}}{2}$

So the velocity of approach is given by $\dfrac{{\sqrt 3 u}}{2}$.

Note: It should be remembered that, velocity of point one and two are equal only and only if string is tight and the string length is constant and no deformation in it. Also if velocity of point of contact is at rest the wheel does not drag on the floor and hence there is no dissipates and it keep on rotating till infinite time but this is not the practical case because at the point of contact there is slight deformation causing some energy to release and hence wheel stops after some time if it does not translate.