Question

A thin uniform circular disc of mass M and radius r is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity $\omega$. Another disc of the same dimensions but of mass M/4 is placed gently on the first disc co-axially. Show that angular velocity of the system is $4\omega /5$.

Answer 1

Hint: Find the initial angular momentum of each disc. The angular momentum of the combined system is conserved as no torque is acting on the system. So apply, law of conservation of angular momentum. The angular momentum of the system before and after coupling is conserved.

Formula used:
Angular momentum, $\vec{L}=\vec{I}.\vec{\omega }$

Complete step-by-step answer:
The angular momentum of a rotating system of particle is given by $\vec{L}=\vec{I}.\vec{\omega }$
Where $I$ is the moment of inertia and $\omega $ is the angular velocity of the system about the axis of rotation.
We are given that, a thin uniform circular disc of mass M and radius r is rotating with an angular velocity $\omega$ in a horizontal plane about an axis passing through its centre and is perpendicular to its plane. Its angular momentum can be given as
${{\vec{L}}_{1}}={{\vec{I}}_{disc}}\vec{\omega }=I\omega $
Since, moment of inertia and angular velocity are perpendicular to each other.
Moment of inertia of a uniform circular disc about an axis passing through its centre and is perpendicular to its plane is $\dfrac{1}{2}M{{R}^{2}}$.

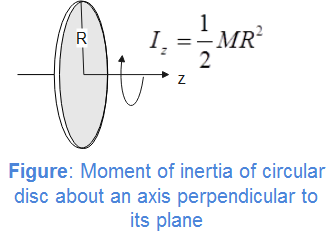
Substituting this value, we obtain angular momentum of disc of mass M initially as
$\left| {{{\vec{L}}}_{1}} \right|=\dfrac{M{{R}^{2}}}{2}\omega $
When another disc of mass M/4 is placed gently on the first disc co-axially, the discs are coupled. Since, no torque is acting on the system, the angular momentum of the system is conserved.
Initially, angular momentum of disc of mass M/4 is
${{L}_{2}}=\dfrac{1}{2}\dfrac{M}{4}{{R}^{2}}\times 0$
When the system is coupled, the mass of the combined disc is $M+\dfrac{M}{4}=\dfrac{5}{4}M$. Let’s assume that angular velocity of coupled system is $\omega '$
The final angular momentum of the combined system is $L'=\dfrac{1}{2}\dfrac{5}{4}M{{R}^{2}}{\omega }'$
Applying conservation of angular momentum, we have
Initial angular momentum of the system = final angular momentum of the system
$L(={{L}_{1}}+{{L}_{2}})=L'$
$\Rightarrow \dfrac{1}{2}M{{R}^{2}}\omega =\dfrac{5}{8}M{{R}^{2}}{\omega }'$
On solving, we get
${\omega }'=\dfrac{4}{5}\omega $
Hence proved.

Note: Moment of inertia of a uniform circular disc about an axis passing through its centre and is perpendicular to its plane is $\dfrac{1}{2}M{{R}^{2}}$. Moment of inertia is a tensor.
If no torque acts on a system, the angular momentum of the system remains conserved.