Question

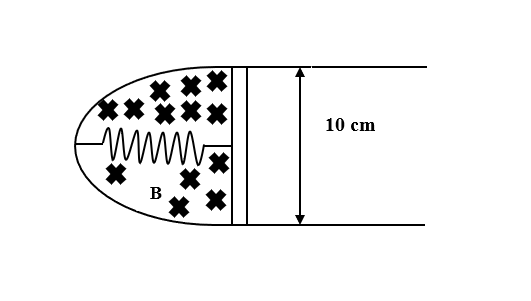
A thin strip 10 cm long is on a U-shaped wire of negligible resistance and it is connected to a spring of spring constant 0.5 ${Nm}^{-1}$ see figure. The assembly is kept in a uniform magnetic field of 0.1 T. If the strip is pulled from its equilibrium position and released, the number of oscillations it performs before its amplitude decreases by a factor of e is N. If the mass of the strip is 50 grams, its resistance $10 \Omega$ and air drag negligible, N will be close to

A. 50000
B. 5000
C. 10000
D. 1000

Answer 1

Hint: To solve this problem, use the formula for force in terms of mass and acceleration. Then, find the force on a spring kept in a uniform magnetic field. Substitute this force in the formula for force in terms of mass and acceleration and also the value of current in terms of magnetic field. Then, write this formula in the form of a differential equation and find its general solution. Solve this solution in such a way that you get the value of t. Then, use the formula for the period of oscillation. Substitute the values and find the period of oscillation. Take the ratio of t and period of oscillation. This will give the number of oscillations.
Formula used:
$F= ma$
$F= -kx – ilB$
$i= \dfrac {Bl}{R}\dfrac {dx}{dt}$
$T= 2\pi \sqrt{\dfrac {m}{k}}$

Complete answer:
Given: l= 10 cm= 0.1 m
            Spring constant (k)= 0.5 N/m
           B= 0.1 T
            Mass of the strip (m)= 50 g= 0.05 kg
           Resistance (R)= $10 \Omega$
Force is given by,
$F= ma$ …(1)
The force on a spring kept in a uniform magnetic field is given by,
$F= -kx – ilB$ …(2)
Substituting equation. (2) in equation.(1) we get,
$-kx-ilB= ma$
We can write the above equation as,
$-kx- ilB= \dfrac {m{d}^{2}x}{d{t}^{2}}$ …(3)
We know, Current in terms of magnetic field can be written as,
$i= \dfrac {Bl}{R}\dfrac {dx}{dt}$ …(4)
Substituting equation. (4) in equation.(3) we get,
$-kx- \dfrac {{B}^{2}{l}^{2}}{R} \dfrac {dx}{dt}= \dfrac {m{d}^{2}x}{d{t}^{2}}$
$\Rightarrow \dfrac {m{d}^{2}x}{d{t}^{2}}+kx + \dfrac {{B}^{2}{l}^{2}}{R} \dfrac {dx}{dt}= 0$
The general solution of the above equation is
$A= {A}_{0} {e}^{-kt}$
Where, $k=\dfrac {{B}^{2}{l}^{2}}{2Rm}$
Now, consider $A= \dfrac {{A}_{0}}{e}$ then kt=1.
$\therefore (\dfrac {{B}^{2}{l}^{2}}{2Rm})t= 1$
Rerranging the above equation we get,
$t= \dfrac {2Rm}{{B}^{2}{l}^{2}}$
Substituting the values in above equation we get,
$t= \dfrac {2 \times 0.05 \times 10}{{0.1}^{2} \times {0.1}^{2}}$
$\Rightarrow t= {10}^{4}s$
The period of oscillation is given by,
$T= 2\pi \sqrt{\dfrac {m}{k}}$
Substituting the values in above equation we get,
$T= 2\pi \sqrt{\dfrac {0.05}{0.5}}$
$\Rightarrow T= \dfrac {2 \pi}{\sqrt {10}}$
$\Rightarrow T=1.987$
Number of oscillations can be given by,
$N= \dfrac {t}{T}$
Substituting the values in above equation we get,
$N= \dfrac {{10}^{4}}{1.987}$
$\Rightarrow N= 5032$
$\Rightarrow N \approx 5000$
Hence, N is close to 5000.

So, the correct answer is “Option B”.

Note:
Before solving the problem, students should look at the units whether those are balanced or not. If the units are not mentioned then convert them before applying them. Here, by number of oscillations we mean frequency of oscillation. The period of oscillation does not depend on how far the spring was initially extended i.e. amplitude. It is also independent of the phase angle. Stiff springs give larger restoring force and hence result in larger acceleration. Thus, has a shorter period.