
A thin rod is bent in the shape of a small circle of radius \[r\]. If the charge per unit length of the rod is \[\sigma \], and if the circle is rotated about its axis at a rate of \[n\] rotations per second, the magnetic induction at a point on the axis at a large distance \[y\] from the centre is?
A) \[{{\mu }_{o}}\pi {{r}^{3}}n\dfrac{\sigma }{{{y}^{3}}}\]
B) \[2{{\mu }_{o}}\pi {{r}^{3}}n\dfrac{\sigma }{{{y}^{3}}}\]
C) \[\dfrac{{{\mu }_{o}}}{4\pi }{{r}^{3}}n\dfrac{\sigma }{{{y}^{3}}}\]
D) \[\dfrac{{{\mu }_{o}}}{2\pi }{{r}^{3}}n\dfrac{\sigma }{{{y}^{3}}}\]
Answer
585.6k+ views
Hint: We will use the theorem of Magnetic Induction which is derived from the Biot Savart Law which in turn states that magnetic field occurs on an object when electric current is passed through its surface area. Hence, to find the mathematical induction, we need to find the current that is following through the circular thin rod in terms of number of turns, circumference and charge per unit length. And then we will place that in the mathematical induction formula along with the area of the circular rod.
The formula for the current flowing in the circular rod is:
\[i=n\times \sigma \times (2\pi r)\]
The formula for the mathematical induction in a circular rod is:
\[B=\dfrac{{{\mu }_{o}}iA}{4\pi \sin t}\]
where \[{{\mu }_{o}}\] is the magnetic constant, \[i\] is the current flowing in the circular rod, \[A\] is the area of the circular rod, \[t\] is the angle formed between point \[y\] to the edge of the circle and the diameter of the circular rod.
Complete step by step solution:
Let us draw a diagram to simplify the position of the length and the current that is flowing in the circular rod:
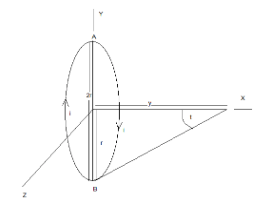
Let us first find the angle \[t\], the value of the angle \[t\] is the length \[y\] as base and \[r\] as the height, we also need to know the hypotenuse, which we will find by the square-root of the sum of \[\sqrt{{{y}^{2}}+{{r}^{2}}}\]. Now as for the value of \[t\], or \[\sin t\] in this case we will place the values in the trigonometric identity of \[\sin \] as \[\sin t=\dfrac{\text{height}}{\text{hypotenuse}}\]: \[\sin t=\dfrac{r}{\sqrt{{{y}^{2}}+{{r}^{2}}}}\]
Let us keep the value of \[\sin t\] aside and let us focus on the current that flows through the circle.
Now let us find the current that is passing in the circular rod, the formula for the current of the circular rod is:
\[i=n\times \sigma \times (2\pi r)\]
The number of turns as given in the question is \[n\].
The circumference of the circular rod with \[r\] as the radius is given as \[2\pi r\]
Hence, the current flowing is \[i=n\times \sigma \times 2\pi r\]
Thereby, let us place all the values in the formula of the magnetic induction, we get the value as:
\[B=\dfrac{{{\mu }_{o}}iA}{4\pi \sin t}\]
\[B=\dfrac{{{\mu }_{o}}\times \left( n\times \sigma \times 2\pi r \right)\times \pi {{\left( r \right)}^{2}}}{4\pi \dfrac{r}{\sqrt{{{y}^{2}}+{{\left( r \right)}^{2}}}}}\] (Area of the circular rod: \[A=\pi {{r}^{2}}\])
Reducing and simplifying the above formula, we get the final result as:
\[B=\dfrac{{{\mu }_{o}}\times \left( n\times \sigma \times 2\pi r \right)\times {{r}^{2}}}{4\times r}\times \sqrt{{{y}^{2}}+{{r}^{2}}}\]
\[\Rightarrow \dfrac{{{\mu }_{o}}\times \left( n\times \sigma \times \pi a \right)\times {{r}^{2}}}{4r}\times {{\left( {{y}^{2}}+{{r}^{2}} \right)}^{\dfrac{3}{2}}}\]
\[\Rightarrow \dfrac{{{\mu }_{o}}n\sigma \pi {{r}^{3}}}{{{y}^{3}}}\]
Therefore, the magnetic induction of the circular rod is \[B=\dfrac{{{\mu }_{o}}n\sigma \pi {{a}^{3}}}{{{y}^{3}}}\]
Note: Students may go wrong while solving the value of the current and then the placing of the current in the mathematical induction, as you can see that the current here is simply the product of charge per unit length with the number of turns. Now per unit length of the circle means the circumference hence, if charge per unit length is \[\sigma \] then the whole circle will be \[\sigma \times \] Total length and that total length is the circumference of the circle. Another thing to keep in mind is the area of the circular rod which will be \[A=\pi {{r}^{2}}\].
The formula for the current flowing in the circular rod is:
\[i=n\times \sigma \times (2\pi r)\]
The formula for the mathematical induction in a circular rod is:
\[B=\dfrac{{{\mu }_{o}}iA}{4\pi \sin t}\]
where \[{{\mu }_{o}}\] is the magnetic constant, \[i\] is the current flowing in the circular rod, \[A\] is the area of the circular rod, \[t\] is the angle formed between point \[y\] to the edge of the circle and the diameter of the circular rod.
Complete step by step solution:
Let us draw a diagram to simplify the position of the length and the current that is flowing in the circular rod:
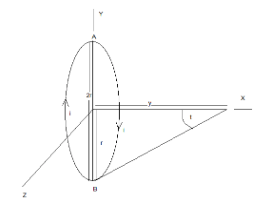
Let us first find the angle \[t\], the value of the angle \[t\] is the length \[y\] as base and \[r\] as the height, we also need to know the hypotenuse, which we will find by the square-root of the sum of \[\sqrt{{{y}^{2}}+{{r}^{2}}}\]. Now as for the value of \[t\], or \[\sin t\] in this case we will place the values in the trigonometric identity of \[\sin \] as \[\sin t=\dfrac{\text{height}}{\text{hypotenuse}}\]: \[\sin t=\dfrac{r}{\sqrt{{{y}^{2}}+{{r}^{2}}}}\]
Let us keep the value of \[\sin t\] aside and let us focus on the current that flows through the circle.
Now let us find the current that is passing in the circular rod, the formula for the current of the circular rod is:
\[i=n\times \sigma \times (2\pi r)\]
The number of turns as given in the question is \[n\].
The circumference of the circular rod with \[r\] as the radius is given as \[2\pi r\]
Hence, the current flowing is \[i=n\times \sigma \times 2\pi r\]
Thereby, let us place all the values in the formula of the magnetic induction, we get the value as:
\[B=\dfrac{{{\mu }_{o}}iA}{4\pi \sin t}\]
\[B=\dfrac{{{\mu }_{o}}\times \left( n\times \sigma \times 2\pi r \right)\times \pi {{\left( r \right)}^{2}}}{4\pi \dfrac{r}{\sqrt{{{y}^{2}}+{{\left( r \right)}^{2}}}}}\] (Area of the circular rod: \[A=\pi {{r}^{2}}\])
Reducing and simplifying the above formula, we get the final result as:
\[B=\dfrac{{{\mu }_{o}}\times \left( n\times \sigma \times 2\pi r \right)\times {{r}^{2}}}{4\times r}\times \sqrt{{{y}^{2}}+{{r}^{2}}}\]
\[\Rightarrow \dfrac{{{\mu }_{o}}\times \left( n\times \sigma \times \pi a \right)\times {{r}^{2}}}{4r}\times {{\left( {{y}^{2}}+{{r}^{2}} \right)}^{\dfrac{3}{2}}}\]
\[\Rightarrow \dfrac{{{\mu }_{o}}n\sigma \pi {{r}^{3}}}{{{y}^{3}}}\]
Therefore, the magnetic induction of the circular rod is \[B=\dfrac{{{\mu }_{o}}n\sigma \pi {{a}^{3}}}{{{y}^{3}}}\]
Note: Students may go wrong while solving the value of the current and then the placing of the current in the mathematical induction, as you can see that the current here is simply the product of charge per unit length with the number of turns. Now per unit length of the circle means the circumference hence, if charge per unit length is \[\sigma \] then the whole circle will be \[\sigma \times \] Total length and that total length is the circumference of the circle. Another thing to keep in mind is the area of the circular rod which will be \[A=\pi {{r}^{2}}\].
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers




