Question

A thin prism of angle 15 made of glass of refractive index ${{\mu }_{1}}=1\cdot 5$is combined with another prism of glass of refractive index ${{\mu }_{2}}=1\cdot 75$. The combination of the prism produces dispersion without deviation. The angle of second prism should be
(A) 7
(B) 10
(C) 12
(D) 5

Answer 1

Hint : Prism is a portion of transparent medium bounded by two plane faces inclined to each other at a suitable angle. We can find angles by using the concept of refraction through a prism.
DISPERSION: Dispersion of a light is the phenomenon of splitting of a beam of white light into its constituent colors on passing through a prism. It is caused because each color has its own characteristics wavelength$\left( \lambda \right)$.
FORMULA USED:
$\delta =\left( \mu -1 \right)A$
$\mu =$Refractive index
A = Angle
$\delta \text{= }$Deviation

Complete step by step answer
A ray of light suffers two refractions on passing through a prism and hence deviates through a certain angle from its original path, but in our case we have two prisms. So, there will be no bending of light that is light will not deviate from its path when it crosses the combination of prisms.

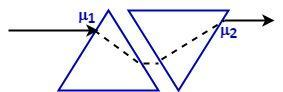
Let us consider deviation of light from first prism is given as:
${{\delta }_{1}}=\left( {{\mu }_{1}}-1 \right){{A}_{1}}\text{ }......\text{(1)}$
For second prism is:
${{\delta }_{2}}=({{\mu }_{2}}-1)A{}_{2}\text{ }......\text{(2)}$
We know that there is no deviation in the path of light. Therefore equation (1) and equation (2) should be equal.
i.e.
$\begin{align}
  & {{\delta }_{1}}={{\delta }_{2}} \\
 & ({{\mu }_{1}}-1){{A}_{1}}=({{\mu }_{2}}-1){{A}_{2}}\text{ }......\text{(3)} \\
 & {{\mu }_{\text{1}}}\text{=1}\text{.5} \\
 & {{\mu }_{\text{2}}}\text{=1}\text{.75} \\
 & {{\text{A}}_{\text{1}}}\text{=15}{}^\circ \\
 & {{\text{A}}_{\text{2}}}\text{= ?} \\
\end{align}$
Put these value in equation (3)
We get,
$\begin{align}
  & \left( 1.5-1 \right)15=(1.75-1){{A}_{2}} \\
 & 0.5\times 15=0.75\times {{A}_{2}} \\
 & {{A}_{2}}=\dfrac{0.5\times 15}{0.75} \\
 & =\dfrac{7.5}{0.75} \\
 & {{A}_{2}}=10 \\
\end{align}$
The angle of the second prism is 10.
Therefore, option (B) is correct.

Note
When refracting angle of prism is small $\left( <10 \right)$, the deviation is calculated from the relation
For prisms with bigger refractive angles. We use
$\delta =({{i}_{1}}+{{i}_{2}})-A$
Where$\text{A = }{{\text{r}}_{\text{1}}}\text{ + }{{\text{r}}_{\text{2}}}$
Concept of incident and refracted angle should be clear. For better understanding refer topic refraction through prism and dispersion of light.