Question

A thin flat circular disc is shown. The ratio of the moments of inertia of the disk about the X-axis, Y-axis and Z-axis is

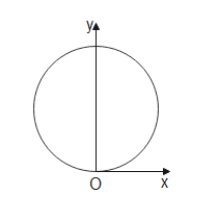
A. $4:1:5$
B. $5:1:6$
C. $2:1:3$
D. $5:1:5$

Answer 1

Hint: The moment of inertia is the tendency of a body to resist changes that result in rotational motion in the body. We need to use the standard formula moment of inertia about an axis passing through its centre of mass of a circular disc and then apply the parallel axis theorem for the required answer.

Complete step by step answer:
So the moment of inertia of a body is the ability of the body to resist changes caused by the application of torque by resisting the change in its angular acceleration. As we know that by using the parallel axis theorem we can find the moment of inertia of the axis passing. For a circular disc, the moment of inertia about an axis as follows
${I_{axis}} = {I_{cm}} + M{d^2}$
Where ${I_{cm}}$ is the moment of inertia about the axis through its centre of mass and $d$ is the distance between the axis and the axis through the centre of mass.

${I_{cm}} = \dfrac{{M{R^2}}}{2}$
Where $M$ is the mass of the disc and $R$ is the radius of the circular disc.
Now we can see that the Z-axis is passing parallelly to the axis through its centre of mass, therefore using the parallel axis theorem we get
${I_z} = {I_{cm}} + M{d^2}$
Substituting the value we get,
$ \Rightarrow {I_z} = \dfrac{{M{R^2}}}{2} + M{R^2}$
$ \Rightarrow {I_z} = \dfrac{{3M{R^2}}}{2}$

Now we can see that the X-axis is passing parallelly to the axis through the diameter of the circular disc. And as we know that the moment of inertia through its diameter is $\dfrac{{M{R^2}}}{4}$ ,
Therefore by applying the parallel axis theorem we get,
${I_x} = \dfrac{{M{R^2}}}{4} + M{R^2}$
$ \Rightarrow {I_x} = \dfrac{{5M{R^2}}}{4}$
Now we can see that the Y-axis is passing through the diameter of the circular disc therefore we get,
${I_y} = \dfrac{{M{R^2}}}{4}$
Now the required ratio would be
$ \therefore {I_x}:{I_y}:{I_z} = 5:1:6$

Hence, option B is correct.

Note: We need to remember the standard moment of inertia of several shapes about the axis through its centre of mass, diameter etc. The moment of inertia of an axis parallel to the axis through its centre of mass is directly proportional to the distance between both the axes always.