Question

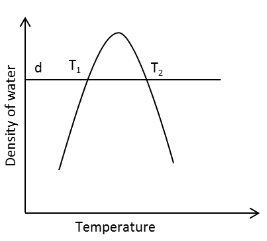
A thermometer uses ‘density of water’ as a thermometric property. The actual reading in the thermometer is ‘height of water’ (h) which is inversely proportional to density of water (d). In a certain temperature range, density of water varies with temperature as shown. The graph is symmetric about the maximum. Two identical bodies (of same mass and specific heat) at different temperatures \[{T_1}\] and \[{T_2}\] show the same reading of height \[{h_1} = {h_2}\] the thermometer. The bodies are brought into contact and allowed to reach thermal equilibrium. The thermometer reading height of water for final equilibrium state \[{h_f}\] satisfies,

A. \[{h_f} = \dfrac{{{h_1} + {h_2}}}{2} = {h_1} = {h_2}\]
B. \[{h_f} > {h_1} = {h_2}\]
C. \[{h_f} < {h_1} = {h_2}\]
D. \[{h_f}\] may be greater or less than \[{h_1} = {h_2}\], depending on the specific heat of bodies
E. Information is not enough

Answer 1

Hint:Use the given relation between the density and height of the water. Derive the relation between the two densities of the two bodies. Guess the temperature of the two bodies in equilibrium and determine the final height of the bodies in equilibrium.

Complete step by step answer:
In the question, it is given that the thermometer shows the reading of height \[h\] of water and the height \[h\] of the water is inversely proportional to the density \[\rho \] of the water.
\[h \propto \dfrac{1}{\rho }\]
\[ \Rightarrow h\rho = {\text{constant}}\] …… (1)
From the given information we can see that the two identical bodies at different temperatures \[{T_1}\] and \[{T_2}\] show the same reading of height \[{h_1} = {h_2}\] the thermometer.
Since the reading of the height \[h\] is the same for two different temperatures \[{T_1}\] and \[{T_2}\] of the two bodies.
Therefore, from equation (1), we can conclude that the density \[{\rho _1}\] and \[{\rho _2}\] of the two bodies is the same.
\[ \Rightarrow {h_1}{\rho _1} = {h_2}{\rho _2}\]
\[ \Rightarrow {\rho _1} = {\rho _2}\]
Also the mass and the specific heat of both the bodies are the same.
Hence, when the body with lower temperature \[{T_1}\] is brought in contact with the second body with the higher temperature \[{T_2}\] and allowed to attain the equilibrium, the hot body loses temperature and the cold body gains the temperature.
In such a way, the two bodies exchange their temperatures and attain the equilibrium.
Hence, the temperature attained by the two bodies is in between the temperatures \[{T_1}\] and \[{T_2}\].
Since the densities \[{\rho _1}\] and \[{\rho _2}\] of both the bodies are the same, the temperature of bodies in equilibrium is the means of their initial temperatures and hence the height attained by the bodies in equilibrium in the final equilibrium state is the means of the two heights which is equal to the heights \[{h_1}\] and \[{h_2}\] as the two bodies have the same mass and specific heat.
We can find that the height \[{h_f}\] in the final equilibrium state is
\[ \therefore {h_f} = \dfrac{{{h_1} + {h_2}}}{2} = {h_1} = {h_2}\]

Hence, the correct option is A.

Note:Since the two bodies have the same mass and specific heat, the heat exchanged i.e. the temperature lost by the hot body and the temperature gained by the cold body is equal. This heat exchange is dependent on their mean temperature.