Question

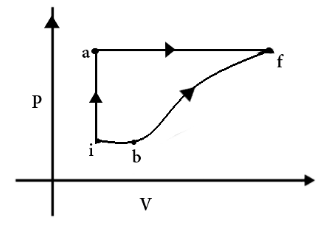
A thermodynamic system is taken from an initial state i, with internal energy \[{U_i} = 100J\] to final state f along two different paths iaf and ibf, as schematically shown in the figure. The work done by the system along the path af, ib, bf are \[{W_{af}} = 200J\], \[{W_{ib}} = 50J\] and \[{W_{bf}} = 100J\] respectively. The heat supplied to the system along the path iaf, ib and bf are \[{Q_{iaf}}\], \[{Q_{ib}}\] and \[{Q_{bf}}\] respectively. If the internal energy of the system in the state b is \[{U_b} = 200J\] and \[{Q_{iaf}} = 500J\], the ratio \[\dfrac{{{Q_{bf}}}}{{{Q_{ib}}}}\] is

Answer 1

Hint : The heat added to the system is the sum of the change in the internal energy and the work done by the system. Work done by a system in a constant volume process is zero.

Formula used: \[dU = dQ - \delta W\], where \[dQ\] is the heat added to the system, \[dU\] is the change in internal energy of the system and \[\delta W\] is the work done by the system.
\[dU = {U_f} - {U_i}\] where \[{U_f}\] is the final internal energy and \[{U_i}\] is the initial internal energy.

Complete step by step answer
Using the first thermodynamic law given as \[dU = dQ - \delta W\] we can write \[{U_{iaf}} = {Q_{iaf}} - {W_{iaf}}\] where the subscripts iaf implies the changes in the variables for the first process.
Also, \[{U_{iaf}} = {U_f} - {U_i}\] where \[{U_f}\] and \[{U_i}\] is the internal energy of state f and i respectively.
\[d{Q_{iaf}}\] is given as 500 J and \[{W_{af}} = {W_{iaf}} = 200J\], since the constant volume process ia has a work done of zero.
Then, from \[{U_{iaf}} = {Q_{iaf}} - {W_{iaf}}\] we get,
\[
  {U_{iaf}} = 500J - 200J \\
   = 300J \\
 \]
Putting this value in equation \[{U_{iaf}} = {U_f} - {U_i}\] and solving we get,
\[
  {U_f} = {U_{iaf}} + {U_i} \\
   \Rightarrow {U_f} = 300 + 100 = 400J \\
 \]
Now, \[{U_{bf}} = {U_f} - {U_b}\]
Thus, \[{U_{bf}} = 400 - 200 = 200J\]
Also, \[{U_{bf}} = {Q_{bf}} - {W_{bf}}\]
\[ \Rightarrow {Q_{bf}} = {U_{bf}} + {W_{bf}}\]
Thus,
\[ \Rightarrow {Q_{bf}} = 200 + 100 = 300J\]
Similarly,
\[
  {Q_{ib}} = {U_{ib}} + {W_{ib}} \\
   \Rightarrow {Q_{ib}} = ({U_b} - {U_i}) + {W_{ib}} \\
 \]
Substituting the values and solving we get,
\[
  {Q_{ib}} = (200 - 100) + 50 \\
   = 150J \\
 \]
Therefore, dividing \[{Q_{bf}}\] by \[{Q_{ib}}\] we get,
\[\dfrac{{{Q_{bf}}}}{{{Q_{ib}}}} = \dfrac{{300}}{{150}} = 2\]

Note
In some text, as you may have seen, the first law of thermodynamic is written as \[dU = dQ + \delta W\] in contrast with \[dU = dQ - \delta W\] as used in the solution above. This may make you confused as to which is more valid. However, both forms are equally valid and correct. The difference lies in the definition of \[W\]. In the form \[dU = dQ + \delta W\], \[W\] is defined as the work done by the system which implies that \[W\] is positive when work is done by the system on its surroundings and negative when work is done on the system by the surroundings. But in the form \[dU = dQ - \delta W\], \[W\] is defined as the work done on the system, which implies that \[W\] is positive when work is done on the system, and \[W\] is negative when work is done by the system.