Question

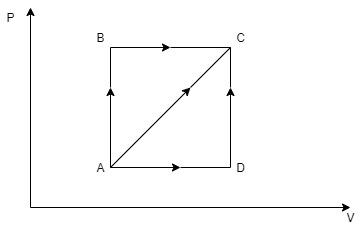
A thermodynamic process is shown in figure. The pressures and volumes corresponding to some points in the figure are ${P_A} = 3 \times {10^4}Pa$, \[{P_B} = 8 \times {10^4}Pa\] and ${V_A} = 2 \times {10^{ - 3}}{m^3}$, ${V_D} = 5 \times {10^{ - 3}}{m^3}$. In process $AB$, $600J$ of heat is added to the system and in process $BC$, $200J$ of heat is added to the system. The change in internal energy of the system in process $AC$ would be:
A) $560J$
B) $800J$
C) $600J$
D) $640J$

Answer 1

Hint:For a thermodynamic process, the total energy is conserved from the first law of thermodynamics. Hence to calculate the change in internal energy of the system one should look at the total change in the heat and the total work done by the system.

Formulae Used:
The total work done by a system is
$W = P \times \left( {{V_{final}} - {V_{initial}}} \right)$..............................(1)
where, $P$is the pressure of the system, ${V_{initial}}$ is the initial volume of the system and $Vfinal$is the final volume of the system after the thermodynamic process.
According to the First law of thermodynamics, in a thermodynamic process involving a closed system, the increment in the internal energy is equal to the difference between the heat accumulated by the system and the work done by it.
So, you can express it mathematically as
$\Delta U = Q - W$...............................(2)
where, $\Delta U$ is the change in the internal energy of the system, $Q$ is the heat accumulated by the system and $W$ is the total work done by the system.
Step by step answer:
Step 1:
In the process $AB$, the volume remains unchanged, that is ${V_A} = {V_B}$.
Calculate the work done in the process $AB$by using eq (1)
$
  {W_{AB}} = P \times \left( {{V_B} - {V_A}} \right) \\
   = P \times 0 \\
   = 0J \\
 $
Step 2:
Identify the accumulated heat of the system in the process $AB$:
${Q_{AB}} = 600J$
Step 3:
In the process $BC$, the pressure remains unchanged, that is to say, ${P_B}$.
Calculate the work done in the process $BC$ by using eq (1)
${W_{BC}} = {P_B} \times \left( {{V_C} - {V_B}} \right)$......................(3)
You already have ${V_B} = {V_A} = 2 \times {10^{ - 3}}{m^3}$
Now, you can see that volume of the system at $C$ is equal to the volume of the system at $D$, hence, ${V_C} = {V_D} = 5 \times {10^{ - 3}}{m^3}$
Now put the values in eq (3).
$
   \Rightarrow {W_{BC}} = 8 \times {10^4} \times \left[ {\left( {5 \times {{10}^{ - 3}}} \right) - \left( {2 \times {{10}^{ - 3}}} \right)} \right]Pa.{m^3} \\
   = 8 \times \left( {5 - 2} \right) \times {10^{\left( {4 - 3} \right)}}Pa.{m^3} \\
   = 8 \times 3 \times 10Pa.{m^3} \\
   = 240Pa.{m^3} \\
   = 240J \\
 $
Step 4:
Identify the accumulated heat of the system in the process $BC$:
${Q_{BC}} = 200J$
Step 5:
Now for closed process$ABC$, you can use the eq (1) to find the change in Internal energy for the process $AC$:
$
  \Delta {U_{AC}} = {Q_{total}} - {W_{total}} \\
   = {Q_{AB}} + {Q_{BC}} - {W_{AB}} - {W_{BC}} \\
   = \left( {600 + 200 - 0 - 240} \right)J \\
   = 560J \\
 $

Final answer:The change in internal energy of the system in the process $AC$ is $\left( A \right)$ $560J$.

Note: You can see that throughout the processes $AB$ and $DC$, the volume of the system remained unchanged. These types of processes are called Isochoric Processes. As you have calculated, for any isochoric process, you can easily start by taking the work done by the system in any isochoric process to be zero. The processes $BC$ and $AD$ happened in constant pressures. This type of process is called Isobaric Process.