Question

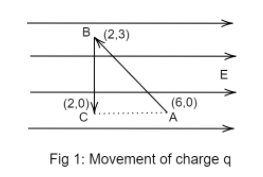
A test charge is moved without acceleration from A to C along the path from A to B and then from B to C in electric field E as shown in the figure.
(i) Calculate the potential difference between A and C.
(ii) At which point of the two is the electric potential more and why?

Answer 1

Hint:
1. The potential difference doesn’t depend on the path taken to displace a charge from one point to another. Electric potential is produced by a conservative electric field. In any conservative field, only starting and endpoints matter to define potential not the path.
2. In the direction of the field, a point that is nearer to the source or located earlier along the field lines generally has a higher potential than other.

Formula used:
1. Two-point distance formula in 2D:\[d = \sqrt {{{({x_{final}} - {x_{initial}})}^2} + {{({y_{final}} - {y_{initial}})}^2}} \]
Where, $d$ is the distance between two points
And
2. Electric field
$E = \dfrac{{ - dV}}{{dx}}$ ……(1)
where,
$V$ is the potential.
$x$ is the displacement.

Complete step by step solution:
Given:
The charge is displaced as in fig 1.
Electric field = $E$
We need to find the potential difference between $A$ and $C$.
(i) Find the displacement of the charge:
Distance between point $A$ and $C = 2 - 6$
Distance between point $A$ and $C = -4$
Rearrange eq (1) to get:
$Edx = - dV$
Integrate for the total displacement of the charge. As the potential doesn’t depend on the path taken, we can take the limits as ${V_A}$ and ${V_C}$:
\[\int\limits_0^x {Edx} = - \int\limits_{{V_A}}^{{V_C}} {dV} \]
Put $x = - 4$as the displacement from A to C:
$\Rightarrow E( - 4 - 0) = - ({V_C} - {V_A})$
$\Rightarrow {V_C} - {V_A} = 4E $

(ii) We have seen in (i) that ${V_C} - {V_A}$ is a positive quantity. This implies that ${V_C} > {V_A}$.

$\therefore$ (i) The potential difference between $A$ and $C$ is $4E$.
(ii) The potential at point $C$ is more than the potential at point $A$.

Note:
In questions like these, apply the right-hand thumb rule to find the direction of the induced magnetic field. Then apply Lenz’s law to find the induced current generated in the rings to oppose it.