Question

When a test charge is brought from infinity towards the centre along the perpendicular bisector of the electric dipole, what is the work done?

Answer 1

Hint: Here we have to calculate the work done in bringing the charge from infinity to the center of an electric dipole. We know that work done in bringing charge from infinity to some point is given by the product of the charge and the potential of the point. So here we will find potential at the center of the electric dipole, to find the work done.

Complete answer:
Let us first draw the diagram to understand the given situation

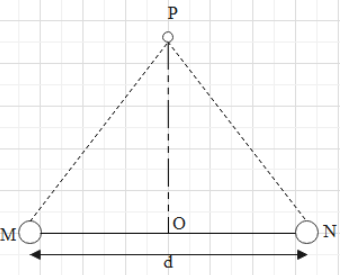
Here MN represents the dipole and O is the center of dipole, P is the test charge along the perpendicular bisector. Now we know that a perpendicular bisector divides the plane equally into two halves. Hence the dipole will become an equipotential surface as potential at side OM will be equal to ON.
Now the work done in bringing a charge from infinity is given by the charge times the potential but for the equipotential surface is zero as the potential difference will be the same all over the surface. Even we can conclude with the diagram that P is equally distant from M and N and it is an electric dipole therefore the charges will be equal and opposite and therefore potential will be zero.
Hence work done in bringing a charge from infinity to the center of dipole will be zero.

Note:
Work done in bringing a charge from one place to another is given as potential difference between two points times the charge. But at infinity potential is zero due to which work done is simply potential at given point times the charge. And here potential at the center of the dipole is zero due to which we get zero work done. Although if we bring charge along a perpendicular bisector we will get the same result, i.e. zero.