Question

A tent of height \[3.3m\] is in the form of a right circular cylinder of diameter 12 m and height \[2.2m\], surmounted by a right circular cone of the same diameter. Find the cost of the canvas of the tent at the rate of \[{\rm{Rs}}.500\] per \[{m^2}\] .

Answer 1

Hint: Here we need to find the cost of canvas required for the tent. We will first find the height of the cone and then we will find the curved surface area of the cylindrical part of the tent using the formula. We will then find the curved surface area of the conical part of the tent using the formula. Then we will add both the curved surface area to get the area of canvas required. We will find the cost of canvas required for the tent by multiplying the area of tent by the given rate.

Complete step-by-step answer:
It is given that:
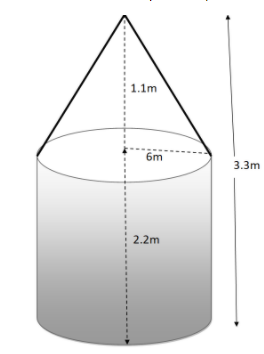
Height of tent \[ = 3.3m\]
Height of the cylindrical part of the tent \[ = 2.2m\]
Therefore, height of the conical part of the tent \[ = 3.3m - 2.2m = 1.1m\]
Diameter of cylindrical part and conical part of the tent \[ = 12m\]
Therefore, the radius of cylindrical part and conical part of the tent \[ = \dfrac{{12m}}{2} = 6m\]
We will first draw the figure of the tent.

Now, we will find the curved surface cylindrical part of the tent.
Substituting \[r = 6\] and \[h = 2.2\] in the formula curved surface area \[ = 2\pi rh\], we get
Curved surface cylindrical part of the tent \[ = 2 \times \dfrac{{22}}{7} \times 6 \times 2.2\]
On multiplying the numbers, we get
\[ \Rightarrow \] Curved surface cylindrical part of the tent \[ = 82.971{m^2}\]
Now, we will find the slant height of the cone.
Substituting \[r = 6\] and \[h = 1.1\] in the formula \[l = \sqrt {{h^2} + {r^2}} \], we get
\[l = \sqrt {{{\left( {1.1} \right)}^2} + {6^2}} \]
On finding the squares, we get
\[ \Rightarrow l = \sqrt {1.21 + 36} \]
Adding the terms, we get
\[ \Rightarrow l = \sqrt {37.21} \]
On further simplification, we get
\[ \Rightarrow l = 6.1m\]
Now, we will find the curved surface area of the conical part of the tent.
Substituting \[r = 6\] and \[l = 6.1\] in the formula curved surface area of the cone \[ = \pi rl\], we get
Curved surface conical part of the tent \[ = \dfrac{{22}}{7} \times 6 \times 6.1\]
On multiplying the numbers, we get
\[ \Rightarrow \] Curved surface conical part of the tent \[ = 115.029{m^2}\]
The total surface area of the tent area will be equal to the sum of curved surface area of conical part of the tent and cylindrical part of the tent
Now, Total surface area of the tent \[ = 82.971{m^2} + 115.029{m^2}\]
On adding the numbers, we get
Total surface area of the tent \[ = 198{m^2}\]
Now, we will calculate the cost of canvas required for the tent by multiplying Total surface area of the tent by the rate of canvas. Therefore, we get
The cost of canvas required for the tent \[ = 500 \times 198 = {\rm{Rs}}.99000\]
Hence, the cost of the canvas required for the tent is Rs 99000.

Note: Here we need to keep in mind that the total area of the tent will be equal to the sum of curved surface area of the conical part of the tent and curved surface cylindrical part of the tent but not the total surface area of the conical part of the tent and the cylindrical part of the tent. This is because the canvas covers only the outside curved surface of the tent and it does not cover the top and base of the cylindrical part from inside. In addition, we need to change the diameter into radius before substituting it in the formula or else we will get the wrong answer.