Question

A teak wood log is cut first in the form of a cuboid of length 2.3m, width 0.75m and a certain thickness. Its volume is $1.104{{m}^{3}}$ . How many rectangular planks of size 2.3m x 0.75m x 0.04m can be cut from the cuboid?

Answer 1

Hint: In order to solve this problem, we need to find all the dimensions of the teak wooden log. Further, we can solve this, we need to find which side is getting cut and then taking the ratio of that particular dimension, we can get the required answer. In this case, we can say that length and width is the same, so the dimension that is cut is thickness.

Complete step-by-step answer:
Let's start by finding the dimensions for the teak wood log.
We have been given the length, width and volume. So we aim to find the thickness of the wooden log.

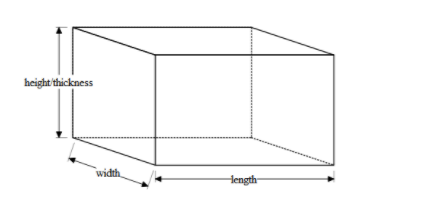
The formula of volume of a cuboid is given by as follows,
$\text{Volume = length }\!\!\times\!\!\text{ width }\!\!\times\!\!\text{ thickness}$
Substituting the values of length = 2.3m, width = 0.75m, and volume =$\text{1}\text{.104}{{\text{m}}^{\text{3}}}$ , we get,
$1.104=2.3\times 0.75\times \,\text{Thickness}$.
Solving for thickness we get,
$\text{Thickness}=\dfrac{1.104}{2.3\times 0.75}=0.64m............(i)$
Hence the dimensions of the teak wood log are length = 2.3m, width = 0.75m and thickness = 0.64m.
The required rectangular planks are of dimensions length = 2.3m, width = 0.75m, thickness = 0.04m.
As we can see that the cut is made perpendicular to the thickness. So, the thickness is the dimension that is sliced down.
We can get to the conclusion that Wooden log thickness = n x Rectangular plank thickness,
where n is the number of planks that can be cut from the cuboid.
Substituting the values, we get,
$0.64=n\times 0.04$
Solving for n we get,
$n=\dfrac{0.64}{0.04}=16$
Therefore, 16 rectangular planks can be formed from the cuboid.

Note: We can solve this problem without finding the thickness of the wooden log. We can get a similar answer if we calculate the ratio of the volume of a wooden log to the volume of rectangular planks.
We can write it as follows
$n=\dfrac{1.104{{m}^{3}}}{2.3m\times 0.75m\times 0.04m}=16$, where n is the required number of rectangular planks to be cut from the cuboid.