Question

A teacher attempting to arrange the students for mass drill in the form of a solid square found that 24 students were left over. When he increased the size of the square by one student, he found he was short of 25 students. Find the number of students.
A. 24
B. 600
C. 480
D. 48

Answer 1

Hint: First assume the side of the square to be x and use that to find the relation between area and the number of students with the help of given conditions. Hence find the total number of students.

Complete Step-by-step answer:

A square is a regular quadrilateral, which means that it has four equal sides and four equal angles.
We also know that if the side of a square is $x$ units, then the area of the square is ${x^2}$ square units.
Given the problem, a teacher is attempting to arrange the students for mass drill in the form of a solid square.
While arranging the student, the teacher found out that the 24 students still remained outside, that is they were not a part of the square.
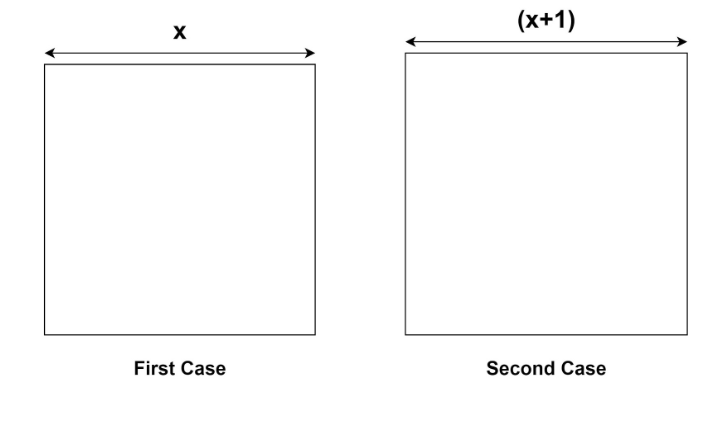
Let the side of the square be formed by $x$ students.
Here one student represents a unit of length for the square.
Then the area of the solid square formed by students $ = {x^2}$
Also, since the students represent one unit of length for the side solid square, hence the number of students must be equal to the area of the square.
 Therefore, Number of students forming square$ = {x^2}$
It is given in the problem that the students remaining outside the square are 24.
Hence total number of students $ = {x^2} + 24$
Now in the second case, the teacher increases the side of the square by one student.
Now the area of the new square will be ${\left( {x + 1} \right)^2}$.
Also, it is given that 25 students are short from completing the square of this new dimension.
Using the same logic as in previous, we calcite the number of students.
Therefore, total number of students $ = {\left( {x + 1} \right)^2} - 25$
Since the numbers of students are fixed in both the scenarios, hence the calculated quantities must be equal.
$ \Rightarrow {\left( {x + 1} \right)^2} - 25 = {x^2} + 24$
Using the square of binomial formula, ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$, in the above equation, we get
$
   \Rightarrow {x^2} + 1 + 2x - 25 = {x^2} + 24 \\
   \Rightarrow 2x = 25 + 24 - 1 = 48 \\
   \Rightarrow x = 24 \\
$
Hence the value of the side of the square comes out to be $x = 24$students.
Therefore, the total number of students$ = {x^2} + 24 = {24^2} + 24 = 576 + 24 = 600$.
Hence, option (B). 600 is the correct option.

Note: The verbal text needed to be read and analysed properly in problems like above. It is important to assume the right unknown quantity and obtain their values using the conditions given in problems like above. In the above problem, a student could be compared to a unit square in cartesian plane graph, hence used to form squares.