Question

A taxi leaves the station $X$ for station $Y$, every $10\min $. Simultaneously, a taxi also leaves the station $Y$ for station $X$ every $10\min $. The taxies move at the same constant speed and go from $X$ to $Y$ or vice versa in $2hrs$. How many taxis coming from the other side will meet each taxi on the route from $Y$ to $X$?
$\begin{align}
  & A)10 \\
 & B)11 \\
 & C)12 \\
 & D)23 \\
\end{align}$

Answer 1

Hint: The first taxi starting from station $Y$ will meet the first taxi starting from $X$, exactly at one hour, after both these taxies start their journey. From then on, the first taxi starting from station $Y$ will meet other taxis behind the first taxi starting from $X$, every $5$ minutes. Similarly, every taxi behind $Y$ will meet the first taxi starting from station $X$, every $5$ minutes. Therefore, it is enough for us to calculate the total number of meetings of the first taxi starting from $Y$ with the taxies coming from $X$, as well as the total number of meetings of the first taxi starting from $X$ with the taxies coming from $Y$.

Complete step by step answer:
We are told that a taxi leaves the station $X$ for station $Y$, every $10\min $. Simultaneously, a taxi also leaves the station $Y$ for station $X$ every $10\min $. We are also told that these taxis move at the same constant speed and go from $X$ to $Y$ or vice versa in $2hrs$. We are required to calculate the number of taxies coming from $X$, which meet each taxi going from $Y$.
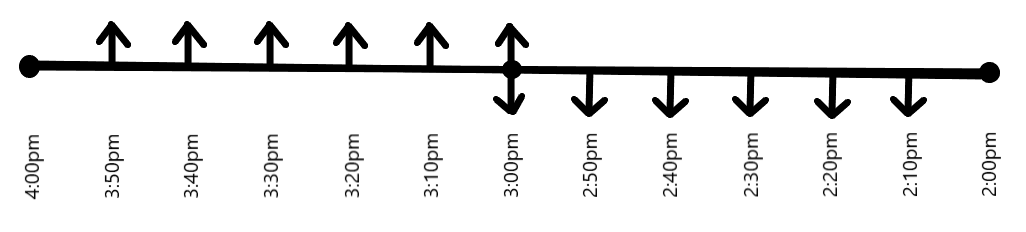
Let us assume that the first taxi starting from $Y$ as well as the first taxi starting from $X$, start at $2:00pm$. Clearly, as provided in the question, these taxies will reach the other stations at $4:00pm$. As we could picture, the first meeting of these first taxies starting from $Y$ and $X$ respectively, happens at $3:00pm$. At $3:00pm$, the first taxi starting from $Y$ and the first taxi starting from $X$ are at the same position on the road as shown in the following figure. It can also be clearly understood from the figure that there are $5$ taxis behind the first cars, on each side of the road.

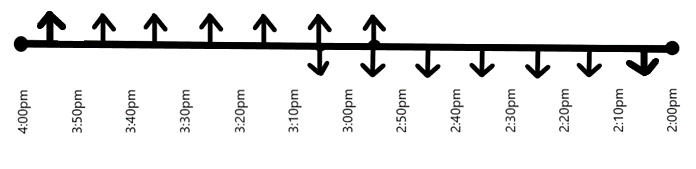
Now, let us consider the movement of first cars starting from station $Y$ and station $X$, during the time between $3:00pm$ and $3:10pm$. Clearly, the first car starting from $Y$ meets the second car starting from $X$, at $3:05pm$. Similarly, the first car starting from $X$ meets the second taxi starting from $Y$ at $3:05pm$, on the other side of the road, as shown in the following figure.

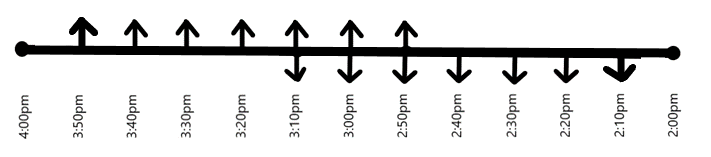
In the next $5$ minutes, the first car starting from $Y$ meets the third car starting from $X$, at $3:10pm$ and the first car starting from $X$ meets the third taxi starting from $Y$ at the same time, on the other side of the road, as shown in the following figure.

Therefore, the total number of meetings of each taxi coming from $X$ with each taxi going from $Y$ during $3:00pm$ and $3:10pm$ is $2+2=4$.
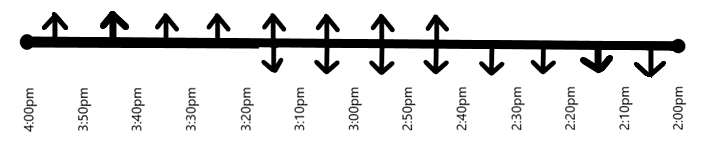
Now, let us consider the movement of first cars starting from station $Y$ and station $X$, during the time between $3:10pm$ and $3:20pm$. Clearly, the first car starting from $Y$ meets the fourth car starting from $X$, at $3:15pm$. Similarly, the first car starting from $X$ meets the fourth taxi starting from $Y$ at $3:15pm$, on the other side of the road, as shown in the following figure.

In the next $5$ minutes, the first taxi starting from $Y$ meets the fifth taxi starting from $X$, at $3:10pm$ and the first taxi starting from $X$ meets the fifth taxi starting from $Y$ at the same time, on the other side of the road, as shown in the following figure.

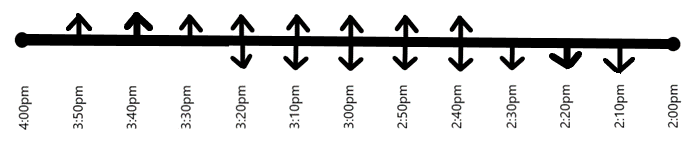
Therefore, the total number of meetings of each taxi coming from $X$ with each taxi going from $Y$ during $3:10pm$ and $3:20pm$ is again $4$.
In the same manner during $3:20pm$ and $4:00pm$, the total number of meetings of each taxi coming from $X$ with each taxi going from $Y$ is $4\times 4=16$.
Therefore, the total number of meetings of each taxi coming from $X$ with each taxi going from $Y$ during $2:00pm$ and $4:00pm$ is given by
$4+4+16-1=23$

Hence, the correct answer is $D$.

Note:
In the last expression, we subtracted $1$ from the total number of meetings because we had counted the meeting of first cars starting from each station twice. (at $3:00pm$) Students may also approach the question in other ways after visualising the process. This question is more of a common-sense question rather than a logical one.