Question

A tank is filled by liquid of density \[\rho \]up to height H. The average pressure on the walls of container is:
A. \[\rho gH\]
B. \[\dfrac{1}{2}\rho gH\]
C. \[\dfrac{1}{4}\rho gH\]
D. \[\dfrac{1}{8}\rho gH\]

Answer 1

Hint: Pressure is defined as the force exerted per area given as \[P = FA\]

In the case of columns of liquid of height H and density \[\rho \]pressure equation is given as \[P = \rho gH\] where g is the gravitational acceleration.

In this question average pressure on the walls of the container now if we find the pressure for a small height of container and if we add the pressure for small height together we can find the pressure on full container.

Complete step by step answer:

Density of the liquid \[\rho \]
Height of the liquid H

We know
Pressure\[P = \rho gH\]

As the container is filled with the liquid up to the height H then the force on the walls by the liquid must be uniform throughout up to a height H, since the force is uniform let us find the force by liquid for a small area \[dA\]

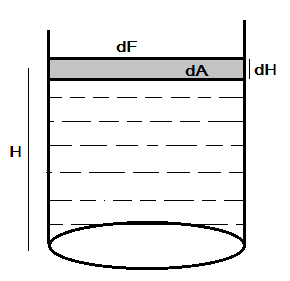
Therefore force on small \[dA\]area will be
\[dF = P.dA - - (i)\],

Where \[P = \rho gH\]and\[dA = 2\pi dH\], hence we can write equation (i) as
\[dF = \left( {\rho gH} \right)\left( {2\pi dH} \right) - - (ii)\]

Since we have got the force on the wall for a small area\[dA\], now let us find the force on wall up to height 0 to H by integrating equation (ii),

\[
  \int\limits_0^F {dF} = \left( {\rho g} \right)2\pi \int\limits_0^H {HdH} \\
  \left[ F \right]_0^F = \left( {\rho g} \right)2\pi \left[ {\dfrac{{{H^2}}}{2}} \right]_0^H \\
  \left( {F - 0} \right) = \pi \rho g\left( {{H^2} - 0} \right) \\
  F = \pi \rho g{H^2} - - (iii) \\
 \]

Since the average pressure is formulated as
Average pressure\[P = \dfrac{F}{A} - - (iv)\]

Now by substitute the value of force from equation (iv) and the area of the tank we get
\[
  P = \dfrac{F}{A} \\
   = \dfrac{{\pi \rho g{H^2}}}{{2\pi H}} \\
   = \dfrac{{\rho gH}}{2} \\
 \]

Hence the average pressure on the walls of container is \[ = \dfrac{{\rho gH}}{2}\]
Option B is correct

Note: Students must know that if we are asked to find the pressure on any uniform container we can find it by finding the pressure for a small area and then adding them together.