
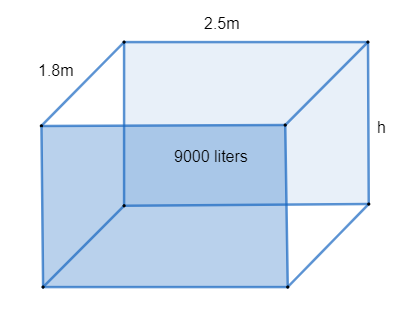
A tank is 2.5m long and 1.8m wide. If the tank contains 9000 liters of water. Find the depth of the water.
(a) 3
(b) 4
(c) 2
(d) 11

Answer
598.2k+ views
Hint: It is said that the tank is 2.5m long, so this is the length of the tank. Similarly we will get the breadth of the tank as the tank is 1.8m wide. Volume of the tank is given as 9000 liters. We know the given tank is a cuboid and the height of the tank can be considered as the depth of water. Use the relation of the volume of cuboid \[V=lbh\] to calculate the depth of water. Lastly, convert the calculated height from m to km.
Complete step by step solution:
We know the tank of water is a cuboid. A cuboid has three dimensions length, breadth and height.
In this case, the height of the tank can be considered as the depth of water.
Following the above said statement we know the given tank of water has length l = 2.5m, breadth b = 1.8m and unknown height h.
Now, the total capacity of any polygon is called its volume.
The volume of \[1{{m}^{3}}\] contains 1 liter of volume.
The given tank of water contains 9000 liters of water therefore the volume \[V=9000{{m}^{3}}\].
We know the formula for volume of a cuboid is given as \[V=lbh\].
Applying the above mentioned formula to find the height of the tank of water we get,
\[V=\left( 2.5 \right)\cdot \left( 1.8 \right)\cdot h\]
By substituting the value of volume V = 9000 in the above expression we get,
\[9000=\left( 2.5 \right)\cdot \left( 1.8 \right)\cdot h\]
On multiplying 2.5 with 1.8 we get the height as,
\[9000=\left( 4.5 \right)\cdot h\]
Dividing the above expression by 4.5 on both sides we get the equation as,
\[\dfrac{9000}{4.5}=h\]
We know that an expression a = b can be written as b = a.
Applying the above mentioned theorem,
\[h=\dfrac{9000}{4.5}\]
Dividing 9000 by 4.5 we get the height as,
h = 2000m
We know that 1km = 1000m.
Applying the same format we will convert the height from m to km.
h = 2km
We get the height as 2 implies the depth of water is 2.
Hence option (c) is the correct answer.
Note: The possible error that you may encounter could be that you might have used any different formula for calculating the volume of the tank instead of using the formula for volume of cuboid. Another error can be that the conversion of height from m to km was not done.
Complete step by step solution:
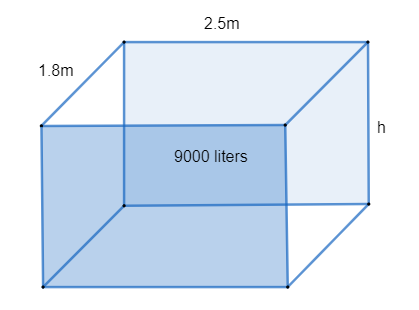
We know the tank of water is a cuboid. A cuboid has three dimensions length, breadth and height.
In this case, the height of the tank can be considered as the depth of water.
Following the above said statement we know the given tank of water has length l = 2.5m, breadth b = 1.8m and unknown height h.
Now, the total capacity of any polygon is called its volume.
The volume of \[1{{m}^{3}}\] contains 1 liter of volume.
The given tank of water contains 9000 liters of water therefore the volume \[V=9000{{m}^{3}}\].

We know the formula for volume of a cuboid is given as \[V=lbh\].
Applying the above mentioned formula to find the height of the tank of water we get,
\[V=\left( 2.5 \right)\cdot \left( 1.8 \right)\cdot h\]
By substituting the value of volume V = 9000 in the above expression we get,
\[9000=\left( 2.5 \right)\cdot \left( 1.8 \right)\cdot h\]
On multiplying 2.5 with 1.8 we get the height as,
\[9000=\left( 4.5 \right)\cdot h\]
Dividing the above expression by 4.5 on both sides we get the equation as,
\[\dfrac{9000}{4.5}=h\]
We know that an expression a = b can be written as b = a.
Applying the above mentioned theorem,
\[h=\dfrac{9000}{4.5}\]
Dividing 9000 by 4.5 we get the height as,
h = 2000m
We know that 1km = 1000m.
Applying the same format we will convert the height from m to km.
h = 2km
We get the height as 2 implies the depth of water is 2.
Hence option (c) is the correct answer.
Note: The possible error that you may encounter could be that you might have used any different formula for calculating the volume of the tank instead of using the formula for volume of cuboid. Another error can be that the conversion of height from m to km was not done.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




