Question

A tank $5m$ high is half-filled with water and then it is filled to the top with oil of density $0.85g/c{{m}^{3}}$. The pressure at the bottom of the tank due to these liquids is:

$A)\text{ }1.85gdyne/c{{m}^{2}}$
$B)\text{ 89}.25gdyne/c{{m}^{2}}$
$C)\text{ 462}.5gdyne/c{{m}^{2}}$
$D)\text{ 500g}dyne/c{{m}^{2}}$

Answer 1

Hint: This problem can be solved by using the direct formula for the pressure at the bottom of a tank that is filled with different liquids in terms of the height of each liquid, its density and the acceleration due to gravity. The sum of the pressures due to the liquids will be the total pressure at the bottom of the tank.

Formula used:
$P=h\rho g$

Complete step by step answer:
We will use the formula for the pressure exerted by a liquid at a point inside it. So, let us write the formula.
The pressure $P$ exerted at a point inside a liquid of density $\rho $ at a depth $h$ from its surface is given by
$P=h\rho g$ --(1)
Where $g$ is the acceleration due to gravity.
Now, let us analyze the question.

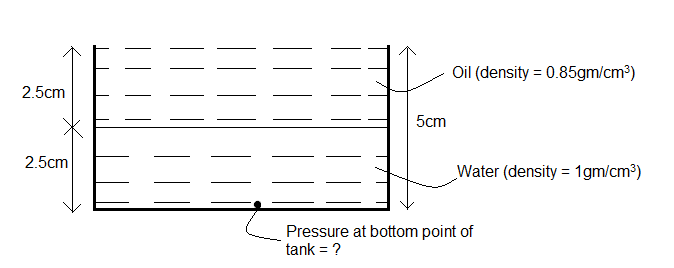
The height of the tank is given to be $5m=500cm$ $\left( 1m=100cm \right)$
Since, the tank is half filled with water and half filled with oil, the height levels of the water and the oil, both will be $h=\dfrac{500}{2}=250cm$.
The density of water is ${{\rho }_{water}}=1g/c{{m}^{3}}$.
The density of oil is ${{\rho }_{oil}}=0.85g/c{{m}^{3}}$.
Let the pressure at the required point due to the oil be ${{P}_{oil}}$.
Let the pressure at the required point due to the water be ${{P}_{water}}$.
Therefore, using (1), we get
${{P}_{oil}}=h{{\rho }_{oil}}g$
${{P}_{water}}=h{{\rho }_{water}}g$
Now, the total pressure will be nothing but the sum of these pressures. Therefore, the total pressure will be
${{P}_{total}}={{P}_{oil}}+{{P}_{water}}$
$\therefore {{P}_{total}}=h{{\rho }_{oil}}g+h{{\rho }_{water}}g=hg\left( {{\rho }_{water}}+{{\rho }_{oil}} \right)=250\times g\times \left( 1+0.85 \right)=250\times g\times 1.85=462.5gdyne/c{{m}^{2}}$
Therefore, we have got the required pressure at the bottom of the tank as $462.5gdyne/c{{m}^{2}}$.
Therefore, the correct option is $C)\text{ 462}.5gdyne/c{{m}^{2}}$.

Note:
Students must not think that at the bottom of the tank since only water is present, only the individual pressure exerted by water should be taken into account. Actually, the pressure exerted by the oil as well as the water should be summed up as done in the question. This is because the oil layer exerts a pressure on the water layer which is translated to the bottom of the tank along with the individual pressure that the water applies (the pressure that the water applies in the absence of the oil layer). So, in essence, the total pressure at the bottom should be the sum of the pressures exerted by the water and the oil layers individually.