Question

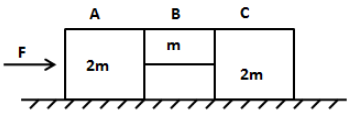
A system is pushed by a force $F$as shown in figure all the surfaces are smooth except between $B$ and $C$. Frictional coefficient between $B$ and $C$ is $\mu $. Minimum value of $F$ to prevent block $B$ from downward slipping is

Answer 1

Hint: In order to deal with this question we have to keep in mind that $B$will not slide shown down if the frictional force is more than the weight of block$B$, so we will find the normal force. The frictional force is the product of the normal force and the coefficient of friction.

Complete step by step answer:
We have given that there are three bodies having masses in the order $2m$, $m$ and $2m$ respectively. Then horizontal acceleration of the system is,
$a = \dfrac{F}{M}$
Here, F is the applied force and M is the total mass of the blocks.
$ a = \dfrac{F}{{2m + m + 2m}}$
$ \Rightarrow a = \dfrac{F}{{5m}}$

Now we will the calculate the normal force between $A$and $B$which will be calculated as,
$N = M \times a$
$ \Rightarrow N = 2m \times \dfrac{F}{{5m}}$
$ \Rightarrow N = \dfrac{{2F}}{5}$
As we know that the frictional force is given by the product of frictional coefficient and the normal force. As for this case we know the frictional coefficient and the normal force so the frictional force is given as:
Frictional force=frictional coefficient $ \times $normal force.
$ \Rightarrow {F_f} = \mu \times N$
$ \Rightarrow {F_f} = \mu \times \dfrac{{2F}}{5}$
From the figure it has been cleared that $B$will not slide down if frictional force is more than the weight of block $B$.

So, the minimum value of $F$ to prevent block $B$ from down ward slipping is given the inequality.
${F_f} \geqslant W$
$ \Rightarrow \mu \dfrac{{2F}}{5} \geqslant Mg$
$ \therefore F \geqslant \dfrac{5}{{2\mu }}mg$

Hence the minimum value of $F$ to prevent block $B$ from down word slipping is $\dfrac{5}{{2\mu }}mg$.

Note:Frictional force refers to the force generated by two surfaces that contact and slide against each other. Thus, forces are mainly influenced by the structure of the surface and the amount of force which needs them together. In the solution, note that the frictional force is directed upwards while the weight of the body is always downwards.