
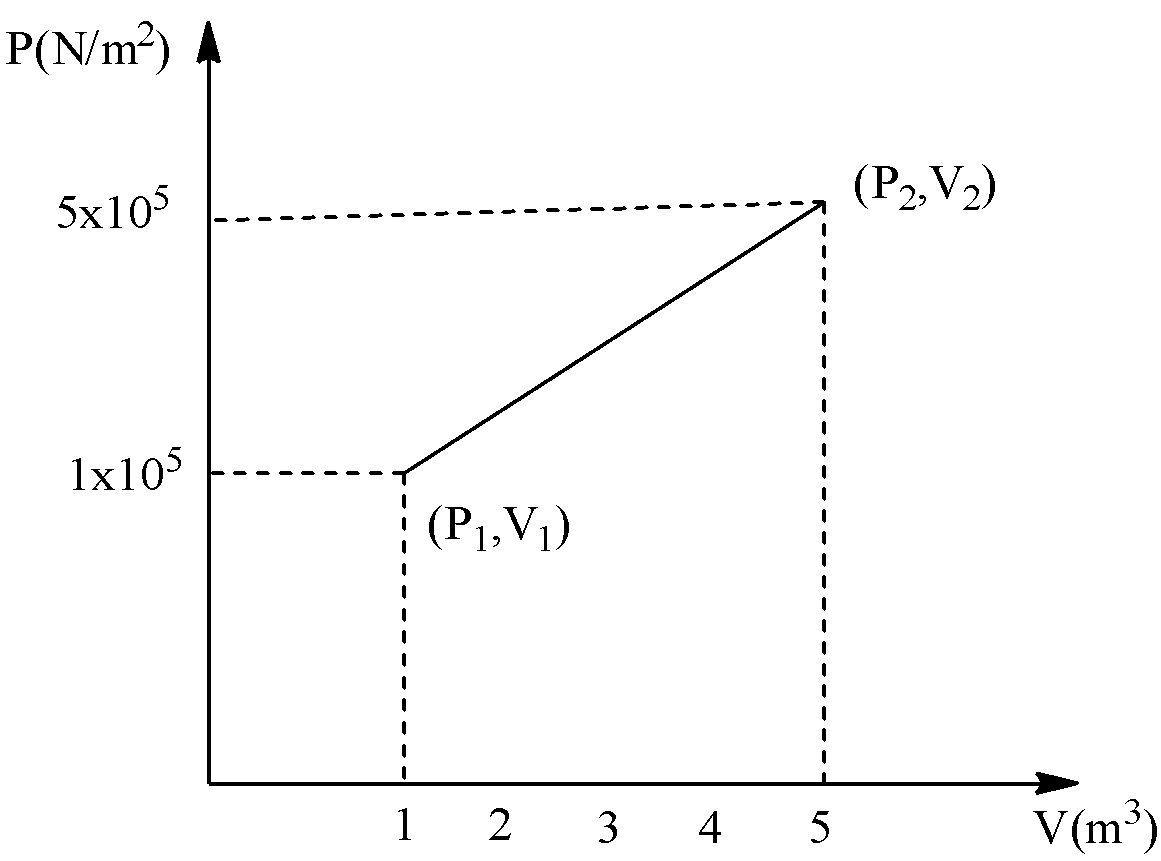
A system changes from the state \[({P_1}{V_1})\] to \[({P_2}{V_2})\] as shown in the figure. What is the word done by the system?
A.\[7.5 \times {10^5}joule\]
B.\[7.5 \times {10^5}erg\]
C.\[12 \times {10^5}joule\]
D.\[6 \times {10^5}joule\]

Answer
503.7k+ views
Hint: We have to know that the work is the energy needed to move an object or any things which are applied against the force. Hence, the energy is the ability to do the work. The works are differentiated into many types. According to thermodynamics, the work is denoted as ‘W’. And it is the method of transfer of energy from one system to another system. The total energy of the system is denoted as, ‘U’ and Q is the heat. In the
chemical systems, the common work is the pressure – volume work, (PV).
Complete answer:
The work done on the system is not equal to \[7.5 \times {10^5}joule\]. Hence, option (A) is incorrect.
The work done is expressed in terms of joule and it is not equal to \[7.5 \times {10^5}erg\]. Hence, option (B) is incorrect.
According to the given graph, it represents the graph of pressure vs volume. The system changes from the state \[({P_1}{V_1})\] to \[({P_2}{V_2})\] . Therefore, the work done of the system is equal to the area under the graph PV.
If we draw a line from the congruent point on one, \[({P_1}{V_1})\] of the given graph, we get a triangle and a rectangle. Let’s see the graph,
Then the work done is equal to the sum of area of the triangle and area of the rectangle.
\[W = \]Area of the triangle + area of the rectangle
Here, the base of the triangle is equal to, \[\left( {5 - 1} \right)\] and height of the triangle is equal to \[\left( {5 - 1} \right)\]. And the base of the rectangle is equal to \[\left( {5 - 1} \right)\] and height of the rectangle is equal to one. Therefore,
\[W = \left[ {\dfrac{1}{2}\left( {5 - 1} \right)\left( {5 - 1} \right)} \right] + \left[ {1 \times \left( {5 - 1} \right)} \right]\]
\[ = \left[ {\dfrac{1}{2} \times 4 \times 4} \right]\left[ {1 \times 4} \right]\]
On simplification we get,
\[ = 12 \times {10^5}joule\]
Hence, option (C) is correct.
The work done on the system is not equal to \[6 \times {10^5}joule\]. Hence, option (D) is incorrect.
Hence, option (C) is correct.
Note:
According to a gas, the work done is the product of pressure and volume, (PV). The pressure may change from \[{P_1}\] to \[{P_2}\] and the volume also changes from \[{V_1}\] to \[{V_2}\]. In the given graph is the pressure vs volume graph. Hence, the work done is equal to the area under the curve and it expresses how the state changes from state one to state two. Therefore, according to thermodynamics, the work done involves when the state of the gas changes from A to B.
chemical systems, the common work is the pressure – volume work, (PV).
Complete answer:
The work done on the system is not equal to \[7.5 \times {10^5}joule\]. Hence, option (A) is incorrect.
The work done is expressed in terms of joule and it is not equal to \[7.5 \times {10^5}erg\]. Hence, option (B) is incorrect.
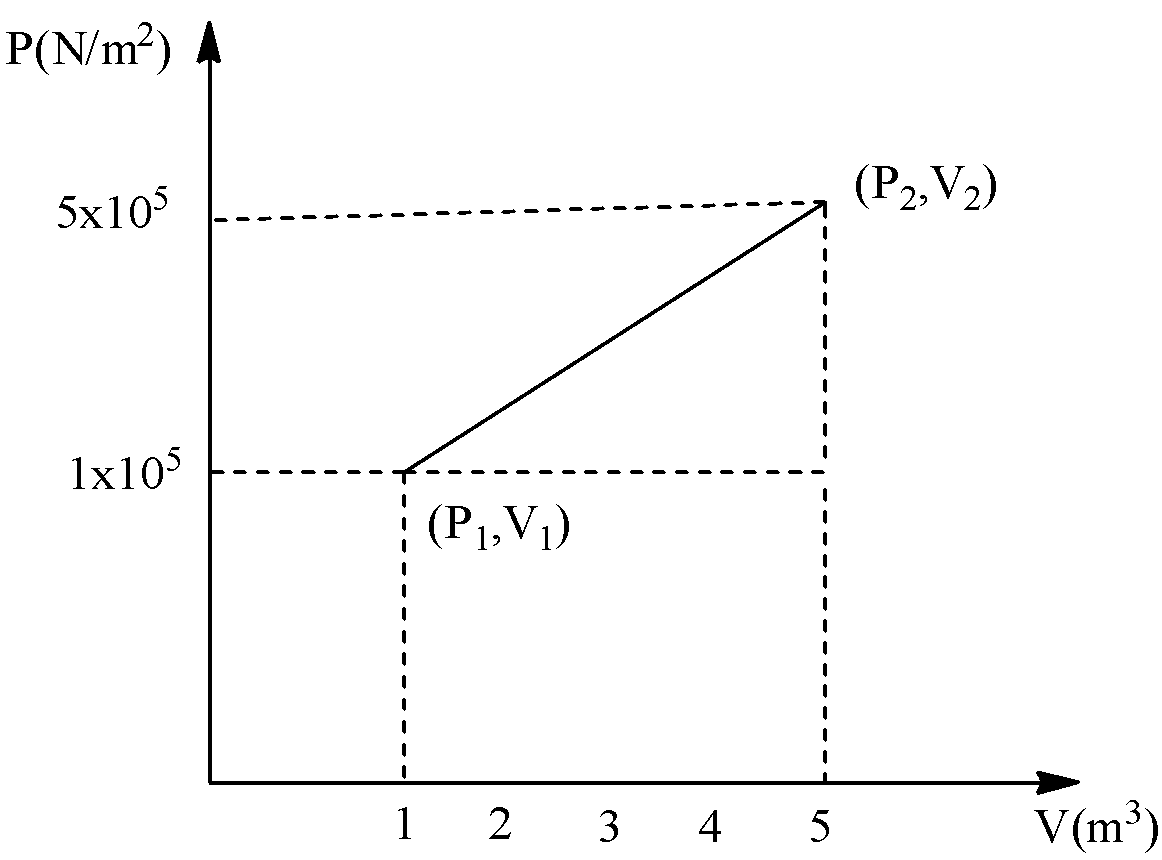
According to the given graph, it represents the graph of pressure vs volume. The system changes from the state \[({P_1}{V_1})\] to \[({P_2}{V_2})\] . Therefore, the work done of the system is equal to the area under the graph PV.
If we draw a line from the congruent point on one, \[({P_1}{V_1})\] of the given graph, we get a triangle and a rectangle. Let’s see the graph,

Then the work done is equal to the sum of area of the triangle and area of the rectangle.
\[W = \]Area of the triangle + area of the rectangle
Here, the base of the triangle is equal to, \[\left( {5 - 1} \right)\] and height of the triangle is equal to \[\left( {5 - 1} \right)\]. And the base of the rectangle is equal to \[\left( {5 - 1} \right)\] and height of the rectangle is equal to one. Therefore,
\[W = \left[ {\dfrac{1}{2}\left( {5 - 1} \right)\left( {5 - 1} \right)} \right] + \left[ {1 \times \left( {5 - 1} \right)} \right]\]
\[ = \left[ {\dfrac{1}{2} \times 4 \times 4} \right]\left[ {1 \times 4} \right]\]
On simplification we get,
\[ = 12 \times {10^5}joule\]
Hence, option (C) is correct.
The work done on the system is not equal to \[6 \times {10^5}joule\]. Hence, option (D) is incorrect.
Hence, option (C) is correct.
Note:
According to a gas, the work done is the product of pressure and volume, (PV). The pressure may change from \[{P_1}\] to \[{P_2}\] and the volume also changes from \[{V_1}\] to \[{V_2}\]. In the given graph is the pressure vs volume graph. Hence, the work done is equal to the area under the curve and it expresses how the state changes from state one to state two. Therefore, according to thermodynamics, the work done involves when the state of the gas changes from A to B.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




