
A swimming pool is 40m long and 15m wide. Its shallow and deep ends are 1.5m and 3m deep respectively. If the bottom of the pool slopes uniformly, find the amount of water in litres required to fill the pool.
a. 42, 33, 000 litres
b. 13, 50, 000 litres
c. 22, 17, 000 litres
d. 41, 12, 000 litres

Answer
525.8k+ views
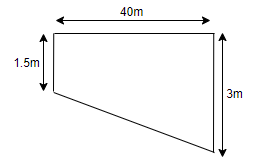
Hint: We will find the volume of the pool as, (area of the pool) $ \times $ (width of the pool). From the figure, we can see that the pool is in the shape of a trapezium, so the area of the pool will be the area of the trapezium, which is, \[\dfrac{1}{2}\left( \text{sum of parallel sides} \right)\left( \text{perpendicular distance between them} \right)\] and also the width of the pool is given as 15m. So, by using these values we will find the volume of the pool, which will be the amount of water required to fill the pool.
Complete step-by-step answer:
It is given in the question that a swimming pool is 40m long and 15m wide. Its shallow and deep ends are 1.5m and 3m deep respectively. If the bottom of the pool slopes uniformly, we are asked to find the amount of water in litres required to fill the pool.
So, from the question we get the following data.
Length of the pool = 40m
Width of the pool = 15m
Height of the shallow end of the pool = 1.5m
Height of the deep end of the pool = 3m
The volume of the pool will give the amount of water required to fill the swimming pool.
So, to find the volume of the pool, we will first find the area of the pool which is in the shape of a trapezium and we will multiply it with the width, that is, 15m.
So, now we know that the area of a trapezium is, \[\dfrac{1}{2}\left( \text{sum of parallel sides} \right)\left( \text{perpendicular distance between them} \right)\]
So, from the figure we can see that the parallel sides are of the length 1.5m and 3m, and the perpendicular distance between these two parallel sides is 40m. So, on substituting these value in the formula of area of trapezium, we get,
$ \begin{align}
& \dfrac{1}{2}\left( 1.5+3 \right)\left( 40 \right) \\
& \dfrac{1}{2}\times 4.5\times 40 \\
& 4.5\times 20 \\
& 90{{m}^{2}} \\
\end{align} $
Hence, we have got the area as $ 90{{m}^{2}} $ . So, now we will find the volume of the pool, which is given by,
(Area of the pool) $ \times $ (Width of the pool)
$ \begin{align}
& 90{{m}^{2}}\times 15m \\
& 1350{{m}^{2}} \\
\end{align} $
So, the volume of the swimming pool is $ 1350{{m}^{3}} $ . And we have to find the amount of water in litres to fill the pool.
So, we know that $ 1{{m}^{3}}=1000l $ . So, we can write,
$ 1350{{m}^{3}}=\left( 1350\times 1000 \right)l=1350000l $
Therefore, we get the amount of water required to fill the pool as 13, 50, 000 litres.
Thus, option (b) is the correct answer.
Note: Many students may make mistakes in the final step by not converting the volume in litres. So, they will lose marks. Also, this question can be solved in an alternative way, by considering the figure as two parts, that is, a rectangle and a triangle as shown below.

So they can find the total volume of the pool as the sum of the volume of the cuboid and the volume of the triangular region. This method can be used if the students forget the formula of the area and volume of a trapezium.
Complete step-by-step answer:
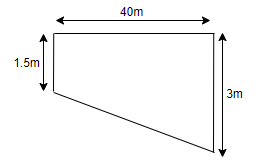
It is given in the question that a swimming pool is 40m long and 15m wide. Its shallow and deep ends are 1.5m and 3m deep respectively. If the bottom of the pool slopes uniformly, we are asked to find the amount of water in litres required to fill the pool.

So, from the question we get the following data.
Length of the pool = 40m
Width of the pool = 15m
Height of the shallow end of the pool = 1.5m
Height of the deep end of the pool = 3m
The volume of the pool will give the amount of water required to fill the swimming pool.
So, to find the volume of the pool, we will first find the area of the pool which is in the shape of a trapezium and we will multiply it with the width, that is, 15m.
So, now we know that the area of a trapezium is, \[\dfrac{1}{2}\left( \text{sum of parallel sides} \right)\left( \text{perpendicular distance between them} \right)\]
So, from the figure we can see that the parallel sides are of the length 1.5m and 3m, and the perpendicular distance between these two parallel sides is 40m. So, on substituting these value in the formula of area of trapezium, we get,
$ \begin{align}
& \dfrac{1}{2}\left( 1.5+3 \right)\left( 40 \right) \\
& \dfrac{1}{2}\times 4.5\times 40 \\
& 4.5\times 20 \\
& 90{{m}^{2}} \\
\end{align} $
Hence, we have got the area as $ 90{{m}^{2}} $ . So, now we will find the volume of the pool, which is given by,
(Area of the pool) $ \times $ (Width of the pool)
$ \begin{align}
& 90{{m}^{2}}\times 15m \\
& 1350{{m}^{2}} \\
\end{align} $
So, the volume of the swimming pool is $ 1350{{m}^{3}} $ . And we have to find the amount of water in litres to fill the pool.
So, we know that $ 1{{m}^{3}}=1000l $ . So, we can write,
$ 1350{{m}^{3}}=\left( 1350\times 1000 \right)l=1350000l $
Therefore, we get the amount of water required to fill the pool as 13, 50, 000 litres.
Thus, option (b) is the correct answer.
Note: Many students may make mistakes in the final step by not converting the volume in litres. So, they will lose marks. Also, this question can be solved in an alternative way, by considering the figure as two parts, that is, a rectangle and a triangle as shown below.

So they can find the total volume of the pool as the sum of the volume of the cuboid and the volume of the triangular region. This method can be used if the students forget the formula of the area and volume of a trapezium.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




