Question

A swimmer crosses a river along a line making an angle of $45^\circ $ with the flow of direction river is $5\,m{s^{ - 1}}$ swimmer takes $12{\text{ seconds}}$ to cross the river of width $60\,m$. Velocity of the swimmer with respect to water will be
A. $5\,m{s^{ - 1}}$
B. $5\sqrt 2 \,m{s^{ - 1}}$
C. $10\,m{s^{ - 1}}$
D. $\dfrac{{5\sqrt 3 }}{3}\,m{s^{ - 1}}$

Answer 1

Hint: First we need to draw a rough diagram. Then with the help of the diagram and given information we can calculate the velocity along the vertical direction or we can say y-axis. The x component is given and now we can write the velocity of the swimmer with respect to water in vector form. Taking its magnitude we can find a solution to this problem.

Complete step by step answer:
As given in the problem, a swimmer crosses a river along a line making an angle of $45^\circ $ with the flow of direction river is $5m{s^{ - 1}}$ swimmer takes $12{\text{ seconds}}$ to cross the river of width $60\,m$. We need to calculate the velocity of the swimmer with respect to water.

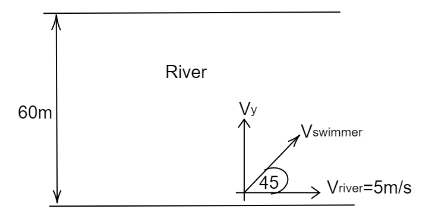
From the diagram we can say, velocity of the river is in horizontal direction hence the x component of the swimmer is equal to the velocity of the river.
So, $V_{\text{river}} = V_x = 5\,m{s^{ - 1}} \ldots \ldots \left( 1 \right)$

Now as per the given information the swimmer crosses the river of width $60\,m$ in $12s$.We can write velocity is equal to distance traveled by the swimmer divided by time taken.Mathematically,
$V_y = \dfrac{d}{t}$
Here,
Velocity along y comenpet is equal to $Vy$
Distance travelled by the swimmer is equal to $d = 60m$
Time taken by the swimmer to cross is equal to $t = 12s$
Putting these velous in the velocity formula we will get,
$V_y = \dfrac{{60m}}{{12s}}$
$ \Rightarrow V_y = 5\,m{s^{ - 1}} \ldots \ldots \left( 2 \right)$
Now we get the two comont of the velocity of the swimmer with respect to water making an angle of $45^\circ $.
$V_{\text{swimmer}} = V_x \,i + V_y \,j$

Now putting equation $\left( 1 \right)$ and $\left( 2 \right)$ in the above formula we will get,
$V_{\text{swimmer}} = 5m{s^{ - 1}}i + 5m{s^{ - 1}}j$
Calculating the magnitude of velocity of the swimmer we will get,
$|V|_{\text{swimmer}} = \sqrt {Vx + Vy} $
$\Rightarrow V_{\text{swimmer}} = \sqrt {Vx + Vy} $
Now putting this values we will get,
$V_{\text{swimmer}} = \sqrt {{{\left( {5m{s^{ - 1}}} \right)}^2} + {{\left( {5m{s^{ - 1}}} \right)}^2}} $
Taking out $5$ as common terms we will get,
$\therefore V_{\text{swimmer}} = 5\sqrt 2 m{s^{ - 1}}$

Therefore the correct option is $\left( B \right)$.

Note: As we can see the direction of the velocity of the river is equal to the velocity of the swimmer along the horizontal direction, we can directly find the solution by equating the velocity of the river with the x component or the horizontal component of the swimmer with respect to the water.