Question

A swimmer can swim in still water with speed $v$ and the river is flowing with velocity $\dfrac{v}{2}$​. To cross the river in the shortest distance, he should swim at an angle \[\theta \] with upstream. Find the ratio of the time taken to swim across the shortest time to that of swimming across over the shortest distance.
A. $\sin \theta $
B. $\cos \theta $
C. $\cot \theta $
D. $\tan \theta $

Answer 1

Hint: We must be aware of the relation between river flow and the flow of objects. This relation gives rise to three conditions with each condition having their specific formulas: minimum time, shortest distance and fastest displacement. Evaluate the given condition and execute the correct formula to get the result. Drawing diagrams will be a better approach.

Complete step by step solution:
Let’s illustrate the given scenario in a diagram:

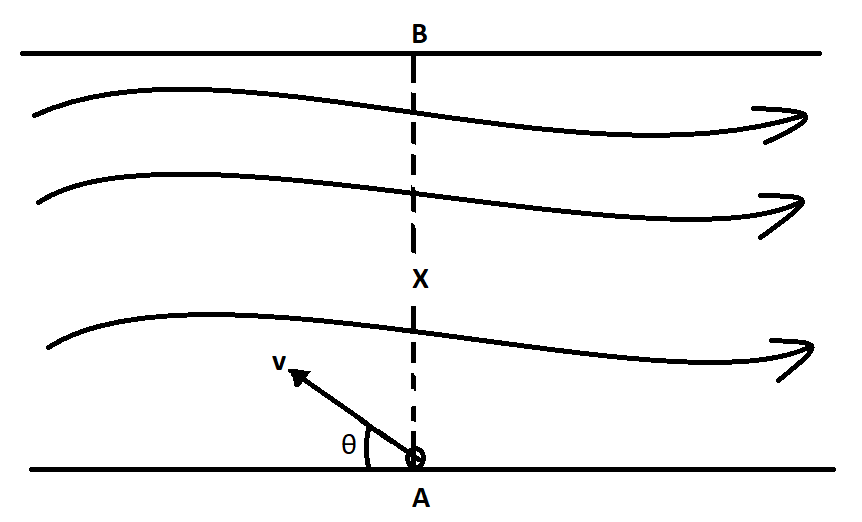
From the above figure it is evident that to cross the river from point A to B, the shortest path to be followed is from A to B directly.
Let this path be =$ x$
According to the question, to travel through the path x, a swimmer needs to start from an angle \[\theta \] with the upstream. The arrow to the right in the figure gives the direction of flow of the river. According to the question, the swimmer goes upstream, so the angle \[\theta \] will be in the opposite direction to the flow of the river.
Evaluation of velocity vector will give velocity of swimmer in direction of shortest path x by

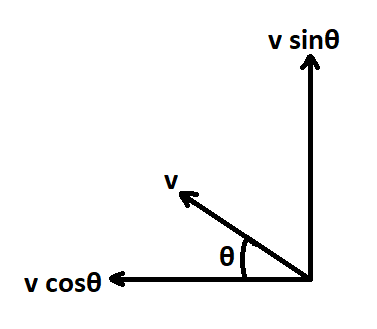
$v' = v\sin \theta $
Where, $v’$=velocity of swimmer for shortest distance
According to formula,
Distance = Speed $ \times $ Time
Calculating time taken by swimmer (assume t) to cross the river following the shortest path using above formula:
${\text{Time = }}\dfrac{{{\text{Distance}}}}{{{\text{Speed}}}}$ ………. (i)
Putting values in the above equation:
$t = \dfrac{x}{{v\sin \theta }}$ …….. (ii)
Let the shortest time required by the swimmer$ = t’$
To cover the river in the shortest time a swimmer needs to swim perpendicular to river flow with maximum velocity.
Using formula (i) we can conclude that:
Minimum time $ = t' = \dfrac{x}{v}$
Let ratio of shortest time to time for shortest distance $= R$
$R = \dfrac{{t'}}{t} = \dfrac{{\dfrac{x}{v}}}{{\dfrac{x}{{v\sin \theta }}}}$
Evaluating above equation will yield
$R = \sin \theta $
$\therefore $ The ratio of the time required to swim across with minimum time to shortest distance is $\sin \theta$.


Note:
On evaluating the velocity of swimmer in vector, velocity vector in plane of flow of river will be affected by the flow of river and velocity vector perpendicular to flow of river will not be affected and is taken as it is evaluated.