Question

A swimmer can swim in still water with speed of $5m{{s}^{-1}}$.While crossing a river his average speed is $3m{{s}^{-1}}$. If he crosses the river in the shortest possible time, what is the speed of flow of water?
$\begin{align}
  & a)2m{{s}^{-1}} \\
 & b)4m{{s}^{-1}} \\
 & c)6m{{s}^{-1}} \\
 & d)8m{{s}^{-1}} \\
\end{align}$

Answer 1

Hint: In the above question we are asked to determine the speed of the flow of water. It is given to us that the swimmer swims such that the time taken for him is the shortest. This implies that he is swimming such that the direction in which he seems to swim is perpendicular to the flow of water. Therefore we will use the magnitude of the vector result to obtain the speed of flow of water.

Formula used: ${{V}_{S}}^{2}={{V}_{A}}^{2}+{{V}_{W}}^{2}$

Complete step by step answer:

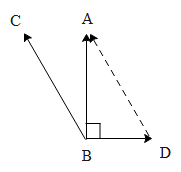
Considering the above figure let us say a swimmer at point B wishes to cross the river such that the time taken is the minimum. Therefore he has to make sure he is moving in a perpendicular path i.e. in the above figure is AB. The direction of the flow of water is BD with speed (${{V}_{W}}$ ). Hence the swimmer actually has to swim with his speed (${{V}_{S}}$) that is still water in direction CB such that he actually moves perpendicular. It is given to us that the average speed of the swimmer in the river is ${{V}_{A}}$ i.e. along path AB. Applying the Pythagoras theorem to the triangle ABD we get,
$\begin{align}
  & {{V}_{S}}^{2}={{V}_{A}}^{2}+{{V}_{W}}^{2} \\
 & \Rightarrow {{5}^{2}}={{3}^{3}}+{{V}_{W}}^{2} \\
 & \Rightarrow {{V}_{W}}^{2}=25-9=16 \\
 & \Rightarrow {{V}_{W}}=4 \\
\end{align}$

So, the correct answer is “Option b”.

Note: It is to be noted that the above problem can be better understood if one considers it as a vector problem itself. The swimmer has to swim with his best speed in direction CB such that the effect of the flow of water makes his path perpendicular. If we consider the above velocities just as some vectors in space, one will understand how the resultant comes.