Question

A survey of 500 television watches produced the following information: 285 watch football, 195 watch hockey, 115 watch basketball, 45 watch football and basketball, 70 watch football and hockey, 50 watch hockey and basketball, 50 do not watch nay of the three games. How many watches all the three games?

Answer 1

Hint: This question belongs to the topic of sets. First of all, we will assume the people watching basketball as set B, the people watching football as set F and the people watching hockey as set H. Then, we will find the number of people who watch any of the three games. When we fill find the number of persons, who watch any of the three games, then we will have to put the values in a given formula and we will get the number of persons who watch all the three games. This will be our final answer.

Complete step by step answer:
The Venn diagram for the above question will be as shown below,

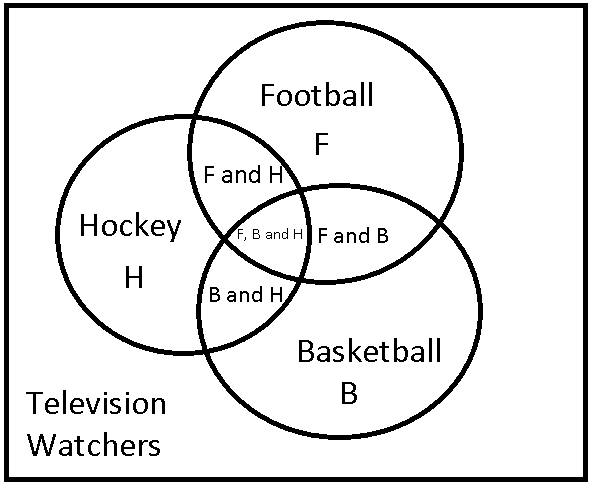
Number of persons who watches TV \[=500\]
Number of people who does not watch any of the three games \[=50\]
Number of people who watches any of the three games = (Number of persons watching TV)- (Number of persons watching any of the three games)
\[\begin{align}
  & =500-50 \\
 & =450 \\
\end{align}\]
Hence, the number of persons who watch any of the three games\[=450=n(B\cup F\cup H)\](let)
Number of persons watching basketball \[=285=n(B)\](let)
Number of persons watching football \[=195=n(F)\](let)
Number of persons watching hockey \[=115=n(H)\](let)
Number of persons watching both basketball and football \[=45=n(B\cap F)\] (let)
Number of persons watching both football and hockey\[=70=n(F\cap H)\](let)
Number of persons watching both hockey and basketball \[=50=n(H\cap B)\](let)
Now, we have to find out the number of persons watching all the three games\[=n(B\cap F\cap H)\]
By using the formula,
\[\begin{align}
  & n(B\cup F\cup H)=n(B)+n(F)+n(H)-n(B\cap F)-n(F\cap H)-n(H\cap B)+n(B\cap F\cap H) \\
 & n(B\cap F\cap H)=-\left( 285+195+115-45-70-50-450 \right) \\
 & n(B\cap F\cap H)=-(-20) \\
 & n(B\cap F\cap H)=20 \\
\end{align}\]
Hence, the total number of persons who watch all the three games is 20.
Note:
 In this question, many students get confused and think about the number of persons who do not watch any of the three games as the persons who watch any of the three games. Also, be careful in putting the formula and the respective values very carefully, as there are very high chances of errors.