Question

A sum of Rs. $6.25$ is made up of $80$ coins which are either $10$ paisa or $5$ paise coins. The number of $10$ paisa and $5$ paise coins are ________ and ______ respectively.

Answer 1

Hint: In this problem we need to calculate the number of $10$ paise coins and number of $5$ paise coins according to the given condition. We have given the sum of $80$coins in rupees. So we will first convert the sum of the $80$ coins into paise by using the relation $1\text{ rupee}=100\text{ paise}$ . now we will assume the number of $10$ paise coins as $x$ and number of $5$ paise coins as $y$ . we have given the total number of coins as $80$. So we will equate the sum of $x$ and $y$ to $80$and consider it as equation one. Now we will sum the value of assumed coins and equate it to the converted value which is in paise. It will become our second equation. By solving the two equations we will get the number of $10$ paise coins and number of $5$ paise coins.

Complete step by step answer:
Given that, the sum of $80$coins is Rs. $6.25$.
Converting the total value which is rupees into paise by using the relation $1\text{ rupee}=100\text{ paise}$, then we will get
$\begin{align}
  & \text{Rs}\text{. }6.25=6.25\times 100\text{ paise} \\
 & \Rightarrow \text{Rs}\text{. }6.25=625\text{ paise} \\
\end{align}$
Let us assume the number of $10$ paise coins as $x$ and the number of $5$ paise coins as $y$.
We have given the total number of coins as $80$. Now the sum of the coins is given by
$x+y=80......\left( \text{i} \right)$
The value of $x$, $10$ paise coins is given by $x\times 10=10x\text{ paise}$ .
The value of $y$, $5$ paise coins is given by $y\times 5=5y\text{ paise}$ .
Total value of the coins is given by $10x+5y$ .
In the problem they have mentioned the total value of coins as Rs. $6.25$, then we will have
$\begin{align}
  & 10x+5y=\text{Rs}\text{. }6.25 \\
 & \Rightarrow 10x+5y=625.......\left( \text{ii} \right) \\
\end{align}$
Performing the operation $\left( \text{ii} \right)-5\left( \text{i} \right)$ to solve the both equations, then we will have
$\begin{align}
  & 10x+5y-5\left( x+y \right)=625-5\left( 80 \right) \\
 & \Rightarrow 10x+5y-5x-5y=625-400 \\
 & \Rightarrow 5x=225 \\
\end{align}$
Dividing the above equation with $5$ on both sides, then we will get
$\begin{align}
  & \dfrac{5x}{5}=\dfrac{225}{5} \\
 & \Rightarrow x=45 \\
\end{align}$
Substituting the above calculated $x$ value in equation $\left( \text{i} \right)$ to find the value of $y$ , then we will have
$\begin{align}
  & 45+y=80 \\
 & \Rightarrow y=80-45 \\
 & \Rightarrow y=35 \\
\end{align}$

Hence the number of $10$paise coins are $45$ and the number of $5$ paise coins are $35$ .

Note: In this problem we can solve the system of equations by using any method like graphical method and substitution method. When we plot the graph of the obtained equation, then the graph will look like as

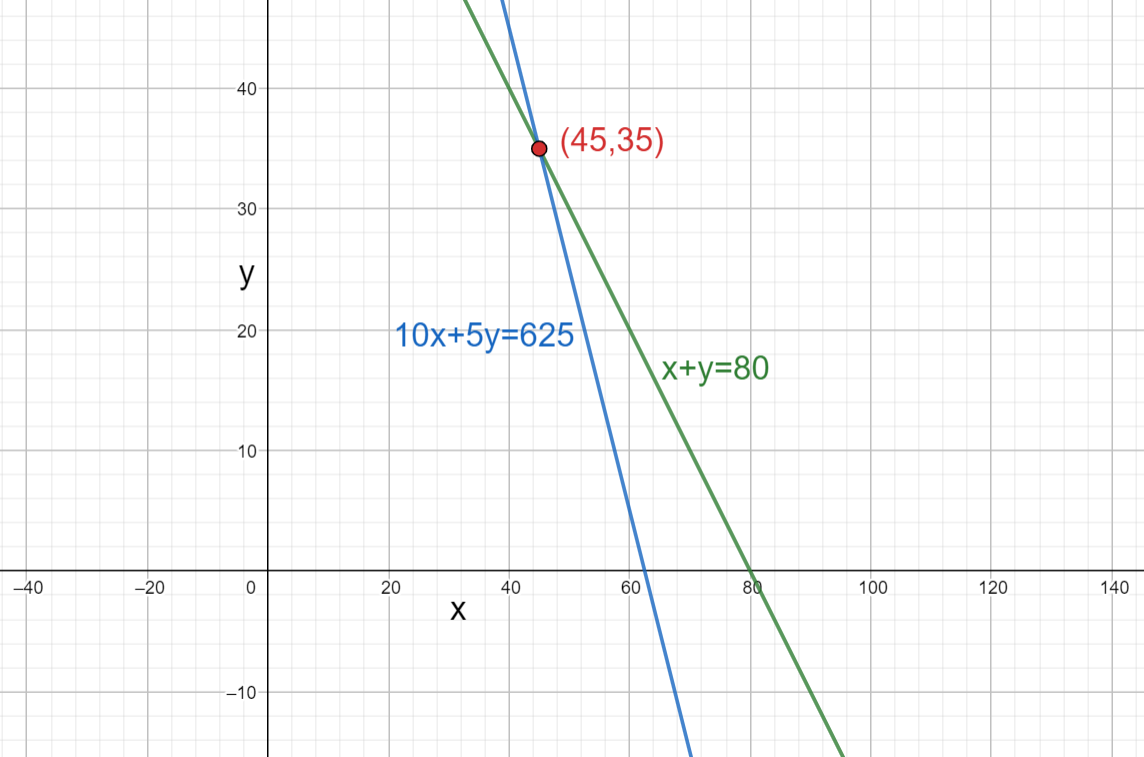
From the graph also we have the solution of the obtained equations as $\left( 45,35 \right)$ .