Question

A sufficiently long beaker with square base of side length $10cm$ is filled with water. If the beaker is accelerated with an acceleration $7.5m/{{s}^{2}}$ . Find:
(i) Angle that the surface of water makes with horizontal
(ii) Final height of water on both sides, i.e., ${{l}_{1}}$ and ${{l}_{2}}$

Answer 1

Hint: Since, the beaker is accelerated horizontally with a constant acceleration, it means that inside the beaker at every point along the horizontal axis , the force varies. This will create an angle that the surface of water will make with the horizontal. This is also the reason behind variable heights of water on both sides of the beaker.

Complete answer:
Let us first try to visualize the given problem with the help of the figure given below:

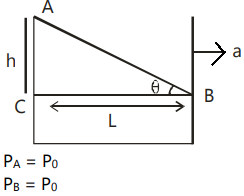
(i) Here, we can see that due to the acceleration $a$ , the surface of water is making an angle $\theta $ with the horizontal.
Therefore,
$\begin{align}
  & \Rightarrow \tan \theta =\left( \dfrac{g}{a} \right) \\
 & \Rightarrow \theta ={{\tan }^{-1}}\left( \dfrac{g}{a} \right) \\
\end{align}$
Or, $\theta ={{\cot }^{-1}}\left( \dfrac{a}{g} \right)$
Given,
$\begin{align}
  & a=7.5m/{{s}^{2}} \\
 & g=10m/{{s}^{2}} \\
\end{align}$
Putting these values in above equation, we get:
$\begin{align}
  & \Rightarrow \theta ={{\cot }^{-1}}\left( \dfrac{7.5}{10} \right) \\
 & \Rightarrow \theta ={{\cot }^{-1}}\left( \dfrac{3}{4} \right) \\
 & \Rightarrow \theta ={{53}^{0}} \\
\end{align}$
Hence, the angle that the surface of water makes with horizontal is ${{53}^{0}}$ .
(ii) Let the initial height of the water column in the beaker be $l$ and the height by which water level drops be $x$ . Then the height by which water level rises at the other end (say $h$ ) can be calculated in terms of $x$ using the conservation of volume of water displaced.
It is given in the problem:
Side length of square base $=10cm$
Now, applying conservation of volume for displaced water:
$\begin{align}
  & \Rightarrow \dfrac{1}{2}\times 10\times (h)\times 10=10\times 10\times x \\
 & \Rightarrow h=2x \\
 & \\
\end{align}$
This implies that rise in water level is equal to the fall in water level, as $h-x=x$.
Now, equating $\tan \theta $ to the ratio of height upon base in $\vartriangle ABC$ , we get:
$\begin{align}
  & \Rightarrow \tan \theta =\dfrac{h}{10} \\
 & \Rightarrow \dfrac{4}{3}=\dfrac{h}{10} \\
 & \Rightarrow h=\dfrac{40}{3}cm \\
\end{align}$
Also, since $x=\dfrac{h}{2}$
 $\begin{align}
  & \Rightarrow x=\dfrac{{}^{40}/{}_{3}}{2}cm \\
 & \Rightarrow x=\dfrac{20}{3}cm \\
\end{align}$
Hence, the final length at the two sides are :
$\begin{align}
  & \Rightarrow {{l}_{1}}=\left( l-\dfrac{20}{3} \right)cm \\
 & \Rightarrow {{l}_{2}}=\left( l+\dfrac{20}{3} \right)cm \\
\end{align}$

Note:
In case of fluid mechanics, whenever the problem has an accelerated frame, we should always first calculate the net force acting upon the fluid. Sometimes, it may come in handy while finding the pressure at any point of the liquid. Also, we saw the use of some very common trigonometric values. So, they should be remembered properly.