Question

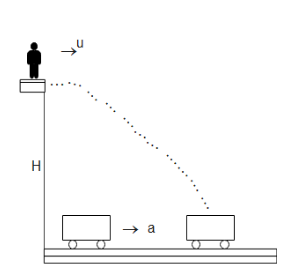
A stunt performer is to run and dive off a tall platform and land in a net in the back of a truck below. Originally the truck is directly under the platform, it starts forward with a constant acceleration $a$ at the same instant the performer leaves the platform is $H$ above the net in the truck, then the horizontal velocity $u$ that the performer must have as he leaves the platform is

Answer 1

Hint: In the given situation a stunt performer at a certain height is about to take a jump and is supposed to fall in the net in the back of a truck. We need to find the initial velocity with which the man should jump so that he could land smoothly on the truck which is accelerating.

Complete step by step answer:
Let us assume that the man takes time $t$ to cover the distance $H$while jumping from the tall platform.Therefore the horizontal distance traveled by him will be,
$s = ut$
Here, $u$ is the initial velocity of the man. And the distance traveled by truck should be the same at the same time so that the man lands in the net in the back of the truck.Therefore for the truck which is accelerating the distance covered will be,
$s = ut + \dfrac{1}{2}a{t^2}$
The initial velocity of the truck is zero therefore
$s = \dfrac{1}{2}a{t^2}$

Now equating both the distances we get
$\dfrac{1}{2}a{t^2} = ut$
Now we will calculate the time $t$
For the man in the vertical direction we have
$H = \dfrac{1}{2}g{t^2}$
Since in the vertical direction the man has zero initial speed and the acceleration caused is due to gravity and the distance of the man in the vertical direction is the height of the platform. Therefore we get,
$t = \sqrt {\dfrac{{2H}}{g}} $
Substituting the value time in the above equation we obtained earlier we get
$ \therefore u = a\sqrt {\dfrac{H}{{2g}}} $

Note: We used the distance formulas for calculating the various distances in the horizontal and the vertical direction. The initial velocity is the velocity of an object in the initial condition and thus the truck has zero initial velocity as it was at rest initially and then started accelerating.