Question

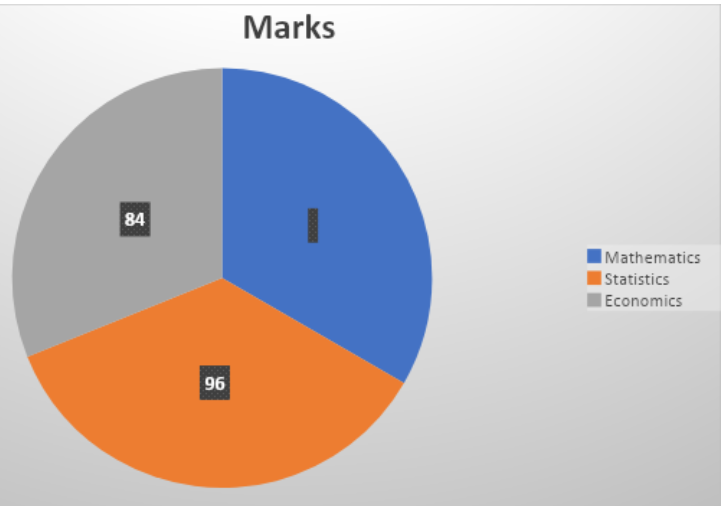
A student represents his score in mathematics, statistics, and economics in a pie chart. The central angle for mathematics is $120{}^\circ $. He scored 96 in statistics and 84 in economics. Find the central angle for statistics.
A. $116{}^\circ $
B. $128{}^\circ $
C. $192{}^\circ $
D. $212{}^\circ $

Answer 1

Hint: First we will try to find the amount of degree allotted to 1 mark and then use a unitary method to find the central angle for the required subject whose marks are mentioned in the question. We find the angles allotted for the other two subjects.

Complete step-by-step solution:
So,$120{}^\circ $ is allotted to mathematics. In a circle, the total central angle is $360{}^\circ $.
As the pie chart only consists of mathematics, economics, and statistics, therefore subtracting the degree allotted to the marks of mathematics from $360{}^\circ $. We will get the degree allotted to the combined marks of statistics and economics.
The allotted angle for statistics and economics is $360{}^\circ -120{}^\circ =240{}^\circ $.
So, the remaining $240{}^\circ $ is allotted to the combined marks of statistics and economics which are 96 and 84 respectively.
Combining the marks, we get $96+84=180$ marks.
So, 180 marks are being allotted to the remaining $240{}^\circ $.
So, using the unitary method we get that for 1 mark the degree allotted is ${{\left( \dfrac{240}{180} \right)}^{{}^\circ }}$.
So, ${{\left( \dfrac{240}{180} \right)}^{{}^\circ }}={{\left( \dfrac{4}{3} \right)}^{{}^\circ }}$.
Now we need to find the central angle for statistics for marks 96 with unitary angle for 1 mark being ${{\left( \dfrac{4}{3} \right)}^{{}^\circ }}$.
So, for 96 marks which is the marks of statistics the degree allotted is ${{\left( \dfrac{4}{3}\times 96 \right)}^{{}^\circ }}={{\left( 4\times 32 \right)}^{\circ }}=128{}^\circ $.

Hence the correct option is B.

Note: While solving these types of problems always try to solve for 1 unit, like in this problem we have calculated the degree allotted to 1 mark and solved for the required marks given in the question to get the desired result.