Question

A string tied on a roof can bear a maximum weight of 50 kg wt. The minimum acceleration that can be acquired by a man of 98 kg to descend will be:
(take g=9.8$m{{s}^{-2}}$).
$\text{A}\text{. }9.8m{{s}^{-2}}$
$\text{B}\text{. 4}.9m{{s}^{-2}}$
$\text{C}\text{. 4}\text{.8}m{{s}^{-2}}$
$\text{D}\text{. 5}m{{s}^{-2}}$

Answer 1

Hint: When the man accelerates downwards, the tension in the string will try to pull the man upwards and the gravity will pull him downwards. Therefore, draw a free body diagram of the man. Equate the net force to ma and put the value of tension equal to the maximum weight. Then find the value of the minimum acceleration.
Formula used:
${{F}_{net}}=ma$

Complete answer:
When the man is descending from the string, the free body diagram will be as shown below.

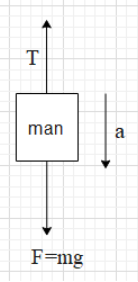
When the man slides down on the string, there will be friction between the man and the rope. The friction will be equal to the tension in the rope. The tension in the rope will try to pull the man upwards. However, the gravitational force will pull the man downwards.
The man can adjust the tension in the string by adjusting his acceleration. However, it is given that the rope can bear a maximum tension of 50 kg wt, which is equal to 50g N (g is acceleration due to gravity).
The magnitude of gravitational force acting on a body of mass m is given as F = mg.
Therefore, the net force on the man is ${{F}_{net}}=F-T=mg-T$.
And from Newton’s second law of motion we know that ${{F}_{net}}=ma$, where a is the acceleration of the body.
$\Rightarrow mg-T=ma$…. (i).
Here, m= 98kg, g = 9.8$m{{s}^{-2}}$. Substitute the value of tension T = 50g = $50\times 9.8N$.
$\Rightarrow 98\times 9.8-(50\times 9.8)=98a$
$\Rightarrow a=\dfrac{98\times 9.8-(50\times 9.8)}{98}=9.8-5=4.8m{{s}^{-2}}$
This means the minimum acceleration that the man must acquire is $4.8m{{s}^{-2}}$.

Hence, the correct option is C.

Note:
Let us understand why a minimum value of acceleration of the man is required.
Consider equation (i), i.e. $mg-T=ma$.
Here, mg and m are constant values. Therefore, as the tension T increases the value of mg-T will decrease. Thus the value of a will increase.
As a result, when the tension reaches its maximum value, the acceleration of the man will be minimum. Therefore, if the man accelerates less than the minimum value the rope will break.