Question

A string is wrapped on a wheel of moment of inertia 0.20 kg.m² and radius 10 cm and goes through a light pulley to support a block of mass 2.0 kg as shown in figure, Find the acceleration of the block?

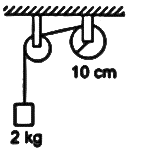
A) 0.89 ms^-2
B) 1.12 ms^-2
C) 0.69 ms^-2
D) none

Answer 1

Hint: Draw the free body diagram considering the tension (T) in it. Convert angular acceleration using $\alpha = \dfrac{a}{r}$

Formula: Torque = (moment of inertia) (angular acceleration) i.e. $T = I\alpha $,
$\alpha = \dfrac{a}{r}$

Complete step by step solution:
T= tension, g = acceleration due to gravity

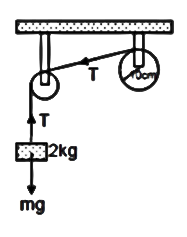
From the free body diagram, we get
mg – T = ma
∴mg=ma + T

Given, m = 2kg, r =10cm=0.1m, I=0.20 kg.m²
Using $T = I\alpha $ and $\alpha = \dfrac{a}{r}$we get,
\[
  mg = ma + I\alpha = ma + I\dfrac{a}{r} \\
   \Rightarrow mg = (m + \dfrac{I}{r})a \\
   \Rightarrow 2 \times 9.8 = (2 + \dfrac{{0.2}}{{0.01}})a \\
   \Rightarrow a = \dfrac{{2 \times 9.8}}{{(2 + \dfrac{{0.2}}{{0.01}})}} = \dfrac{{19.6}}{{22}} = 0.89{\text{ m}}{{\text{s}}^{{\text{ - 2}}}} \\
\]
Therefore, acceleration of the block = 0.89 ms^-2

Correct Answer: A) 0.89 ms^-2

Note: In rotational motion, torque is required to produce an angular acceleration of an object. The amount of torque required to produce an angular acceleration depends on the distribution of the mass of the object. The moment of inertia is a value that describes the distribution.